四川省乐山市2023年初中学业水平考试数学试卷

1. 计算： $\text{[math]}$ （）

A . a B . $\text{[math]}$ C . $\text{[math]}$ D . 1

查看解析收藏纠错

+选题
2. 下面几何体中，是圆柱的为（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列各点在函数 $\text{[math]}$ 图象上的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 从水利部长江水利委员会获悉，截止2023年3月30日17时，南水北调中线一期工程自2014年12月全面通水以来，已累计向受水区实施生态补水约90亿立方米．其中9000000000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 乐山是一座著名的旅游城市，有着丰富的文旅资源．某校准备组织初一年级500名学生进行研学旅行活动，政教处周老师随机抽取了其中50名同学进行研学目的地意向调查，并将调查结果制成如下统计图，如图所示估计初一年级愿意去“沫若故居”的学生人数为（）

A . 100 B . 150 C . 200 D . 400

查看解析收藏纠错

+选题
6. 如图2，菱形ABCD的对角线AC与BD相交于点O，E为边BC的中点，连结OE．若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 2 B . $\text{[math]}$ C . 3 D . 4

查看解析收藏纠错

+选题
7. 若关于x的一元二次方程 $\text{[math]}$ 两根为 $\text{[math]}$ ，且 $\text{[math]}$ ，则m的值为（）

A . 4 B . 8 C . 12 D . 16

查看解析收藏纠错

+选题
8. 我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”，如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形面积为25，小正方形面积为1，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，且 $\text{[math]}$ ，有下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④若点 $\text{[math]}$ 在抛物线上，则 $\text{[math]}$ ．其中，正确的结论有（）

A . 4个 B . 3个 C . 2个 D . 1个

查看解析收藏纠错

+选题
10. 如图5，在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与x轴、y轴分别交于A、B两点，C、D是半径为1的 $\text{[math]}$ 上两动点，且 $\text{[math]}$ ， P为弦CD的中点．当C、D两点在圆上运动时， $\text{[math]}$ 面积的最大值是（）

A . 8 B . 6 C . 4 D . 3

查看解析收藏纠错

+选题

11. 不等式 $\text{[math]}$ 的解集是．

查看解析收藏纠错

+选题
12. 小张在“阳光大课间”活动中进行了5次一分钟跳绳练习，所跳个数分别为：160，163，160，157，160．这组数据的众数为．

查看解析收藏纠错

+选题
13. 如图，点O在直线AB上，OD是 $\text{[math]}$ 的平分线，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

查看解析收藏纠错

+选题
14. 若m、n满足 $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
15. 如图，在平行四边形ABCD中，E是线段AB上一点，连结AC、DE交于点F．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
16. 定义：若x，y满足 $\text{[math]}$ 且 $\text{[math]}$ （t为常数），则称点 $\text{[math]}$ 为“和谐点”．

（1）若 $\text{[math]}$ 是“和谐点”，则 $\text{[math]}$ ．

（2）若双曲线 $\text{[math]}$ 存在“和谐点”，则k的取值范围为．

查看解析收藏纠错

+选题

17. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
18. 解二元一次方程组： $\text{[math]}$

查看解析收藏纠错

+选题
19. 如图，已知AB与CD相交于点O， $\text{[math]}$ ，求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题
20. 如图9，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D为AB边上任意一点（不与点A、B重合），过点D作 $\text{[math]}$ ， $\text{[math]}$ ，分别交AC、BC于点E、F，连结EF．

（1）求证：四边形ECFD是矩形；

（2）若 $\text{[math]}$ ，求点C到EF的距离．

查看解析收藏纠错

+选题
21. 为了践行习近平总书记提出的“绿水青山就是金山银山”的发展理念，某地计划在规定时间内种植梨树6000棵．开始种植时，由于志愿者的加入，实际每天种植梨树的数量比原计划增加了 $\text{[math]}$ ，结果提前2天完成任务．问原计划每天种植梨树多少棵？

查看解析收藏纠错

+选题
22. 为培养同学们爱劳动的习惯，某班开展了“做好一件家务”主题活动，要求全班同学人人参与经统计，同学们做的家务类型为“洗衣”“拖地”“煮饭”“刷碗”．班主任将以上信息绘制成了统计图表，如图所示．

家务类型

洗衣

拖地

煮饭

刷碗

人数（人）

10

12

10

m

根据上面图表信息，回答下列问题：

（1） $\text{[math]}$ ；

（2）在扇形统计图中，“拖地”所占的圆心角度数为；

（3）班会课上，班主任评选出了近期做家务表现优异的4名同学，其中有2名男生．现准备从表现优异的同学中随机选取两名同学分享体会，请用画树状图或列表的方法求所选同学中有男生的概率．

查看解析收藏纠错

+选题
23. 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，与x轴交于点B，与y轴交于点 $\text{[math]}$ ．

（1）求m的值和一次函数的表达式；

（2）已知P为反比例函数 $\text{[math]}$ 图象上的一点， $\text{[math]}$ ，求点P的坐标．

查看解析收藏纠错

+选题
24. 如图，已知 $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ ， D是圆上一点，E是DC延长线上一点，连结AD，AE，且 $\text{[math]}$ ．

（1）求证：直线AE是 $\text{[math]}$ 是的切线；

（2）若 $\text{[math]}$ ， $\text{[math]}$ 的半径为3，求AD的长．

查看解析收藏纠错

+选题
25. 在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动
【问题情境】

刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：

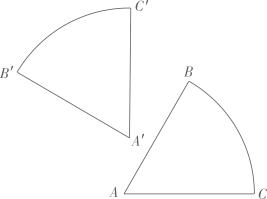
如图，将一个三角形纸板 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 到达 $\text{[math]}$ 的位置，那么可以得到：

$\text{[math]}$ ； $\text{[math]}$ （）

刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键故数学就是一门哲学．

（1）【问题解决】
上述问题情境中“（）”处应填理由：；

（2）如图，小王将一个半径为 $\text{[math]}$ ，圆心角为 $\text{[math]}$ 的扇形纸板ABC绕点O逆时针旋转 $\text{[math]}$ 到达扇形纸板 $\text{[math]}$ 的位置．

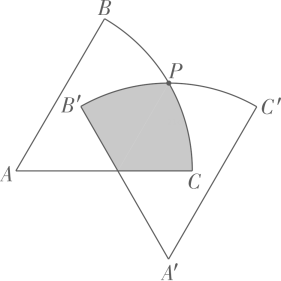
①请在图中作出点O；

②如果 $\text{[math]}$ ，则在旋转过程中，点B经过的路径长为；

（3）【问题拓展】小李突发奇想，将与（2）中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置另一个在孤的中点处固定，然后放开纸板，使其摆动到竖直位置时静止此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．

查看解析收藏纠错

+选题
26. 已知 $\text{[math]}$ 是抛物 $\text{[math]}$ （b为常数）上的两点，当 $\text{[math]}$ 时，总有 $\text{[math]}$

（1）求b的值；

（2）将抛物线 $\text{[math]}$ 平移后得到抛物线 $\text{[math]}$ ．
探究下列问题：

①若抛物线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 有一个交点，求m的取值范围；

②设抛物线C₂与x轴交于A，B两点，与y轴交于点C，抛物线 $\text{[math]}$ 的顶点为点E， $\text{[math]}$ 外接圆的圆心为点F，如果对抛物线 $\text{[math]}$ 上的任意一点P，在抛物线 $\text{[math]}$ 上总存在一点Q，使得点P、Q的纵坐标相等．求EF长的取值范围．

查看解析收藏纠错

+选题

四川省乐山市2023年初中学业水平考试数学试卷

一、选择题：本大题共10个小题，每小题3分，共30分。

二、填空题：本大题共6个小题，每小题3分，共18分。

三、解答题：本大题共10个小题，共102分。解答应写出必要的文字说明，证明过程或演算步骤。

相关试卷收起∨

家务类型	洗衣	拖地	煮饭	刷碗
人数（人）	10	12	10	m

四川省乐山市2023年初中学业水平考试数学试卷

一、选择题：本大题共10个小题，每小题3分，共30分。

二、填空题：本大题共6个小题，每小题3分，共18分。

三、解答题：本大题共10个小题，共102分。解答应写出必要的文字说明，证明过程或演算步骤。

相关试卷 收起∨

相关试卷收起∨