修改时间:2024-07-14 浏览次数:79 类型:中考模拟
|
等级 |
次数 |
频数 |
|
不合格 |
|
|
|
合格 |
|
|
|
良好 |
|
|
|
优秀 |
|
|

请结合上述信息解决下列问题:
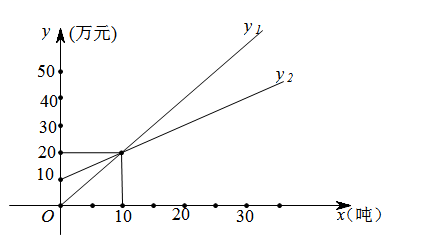
① 的解析式为;
的解析式为.
②当销售量( )满足条件时,该公司盈利(即收入大于成本).
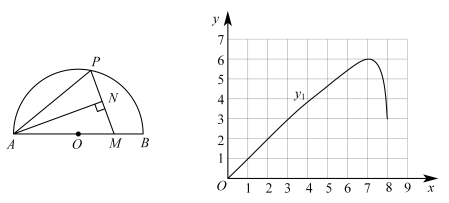
下面是小明的探究过程,请补充完整:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.64 | 7.78 | 7.90 | 8 |
| 0 | 0.99 | 1.99 | 2.97 | 3.92 | 4.82 | 5.61 | 5.90 | 5.56 | 5.18 | 4.46 | 3.30 | 0 |
| 6 | 5.91 | 5.65 | 5.21 | 4.53 | 3.56 | 2.12 | 0.24 | 2.25 | 3.01 | 4.0 | 5.00 | 6 |
请计算,当时,
;
①通过计算可知:;
②通过进一步探究函数图象可知:长度的近似值为
. (保留一位小数)
试题篮