广东省深圳市福田区八校2022-2023学年九年级5月质量检测联考数学试题

修改时间：2024-07-13 浏览次数：1612 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题：(每小题只有一个选项正确，每小题3分，共计30分)

1. -2023的相反数是（）

A . 2023 B . $\text{[math]}$ C . $\text{[math]}$ D . -2023

查看解析收藏纠错

+选题
2. “春雨惊春清谷天，夏满芒夏暑相连……”，我国民间流传有许多“24节气歌”．下面四幅手绘作品，它们依次分别代表“立春”、“芒种”、“白露”、“大雪”四个节气，其中是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 节肢动物门是动物界最大的一门，门下蛛形纲约有60000余种.60000用科学记数法可以表示成（）

A . 0.6×10⁵ B . 6×10⁴ C . 6×10⁵ D . 60×10³

查看解析收藏纠错

+选题
4. 下列计算，正确的是（）

A . (a³)²=a⁶ B . a²·a³=a⁶ C . a⁹÷a³=a³ D . a²-a=a

查看解析收藏纠错

+选题
5. 学校组织部分学生外出开展社会实践活动，安排给九年级三辆车，小敏与小慧都可以从这三辆车中任选一辆搭乘．则小敏与小慧同车的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 网上一些推广“成功学”的主播，常引用下面这个被称为竹子定律的段子：“竹子前4年都用在扎根，竹芽只能长3cm，而且这3cm还是深埋于土下到了第五年，竹子终于能破土而出，会以每天30cm的速度疯狂生长．此后，仅需要6周的时间，就能长到15米，惊艳所有人！”。这段话的确很励志，须不知，要符合算理的话，需将上文“6周”中的整数“6”改为整数（）

A . 5 B . 7 C . 8 D . 9

查看解析收藏纠错

+选题
7. 生活中，我们常用到长方形样、不同型号的打印纸．基于满足影印(放大或缩小后，需保持形状不变)及制作各型号纸张时，既方便又省料等方面的需要，对于纸张规格，存有一些通用的国际标准其中，把A₀纸定义为面积为1平方米，长与宽的比为 $\text{[math]}$ ：1的纸张；沿AO纸两条长边中点的连线裁切，就得到两张A₁纸：再沿A₁纸两条长边中点的连线裁切得A₂纸……依此类推，得A₃ ， A₄ ， A₅等等的纸张(如图1所示)．若设A₄纸张的宽为x米，则x应为（）

A . $\text{[math]}$ B . $\text{[math]}$ 的算术平方根 C . $\text{[math]}$ D . $\text{[math]}$ 的算术平方根

查看解析收藏纠错

+选题
8. 如图2，在两建筑物之间有一旗杆，高15米，从点A经过旗杆顶点恰好可观测到矮建筑物的最底端点C处，从点A测得点C的俯角α为60°，测得点D的俯角β为30°，若旗杆底部G为BC的中点，则，矮建筑物的高CD为（）

A . 18米 B . 20米 C . 10 $\text{[math]}$ 米 D . (45-15 $\text{[math]}$ )米

查看解析收藏纠错

+选题
9. 如图，⊙O的半径为r，交×轴正半轴于点A，直线l垂直平分OA交⊙O于点P，PB⊥y轴于点B．今假设在点O，A处，分别有一质量为m₁ ， m₂的天体(m₁>m₂)；天体物理中把与O，A处于同一平面，坐标为（ $\text{[math]}$ ， $\text{[math]}$ ）的点称为[O，A]系统的拉格朗日4号点，记为L₄ (若把卫星发射到L₄的位置，则卫星会处于相对静止的稳状态)．以下说法中错误的是（）

A . △AOP是等边三角形 B . L₄在线段BP上 C . ∠OL₄A>60° D . 若m₁恒定，则m₂越小，L₄离点P越近

查看解析收藏纠错

+选题
10. 如图，菱形ABCD中，AC交BD于点O，DE⊥AB，垂足为点E，连接OE，若OE=3，AE=7则AC的长为（）

A . 5 $\text{[math]}$ B . 16 C . 10 $\text{[math]}$ D . 12 $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题：(本大题共5小题，每小题3分，共15分)

11. 因式分解：a²-a= ．

查看解析收藏纠错

+选题
12. 若方程x²-4x-5=0的两根为x₁ ， x₂ ，则x₁+x₂=

查看解析收藏纠错

+选题
13. 如图，以矩形ABCD的顶点C为圆心，以任意长为半径作弧，分别交AC及BC的延长线于点E，F，再分别以点E，F为圆心，以大于 $\text{[math]}$ EF的长为半径作弧，两弧交于点H，作射线CH交AD的延长线于点G．若BC=3，AB=4，则DG=

查看解析收藏纠错

+选题
14. 如图，正方形ABCD的顶点A，B分别在y轴，x轴两轴的正半轴上，反比例函数y= $\text{[math]}$ 的图象经过该正方形的中心，若OA=1，OB=2，则k的值为

查看解析收藏纠错

+选题
15. 如图，在Rt△ABC中，AC=BC，点P是BC上一点，BD⊥AP交AP延长线于点D，连接CD．若图中两阴影三角形的面积之差为32(即S_△ACP-S_△PBD=32)，则CD=

查看解析收藏纠错

+选题

三、解答题：(本题共7小题，其中第16题6分，第17题6分，第18题8分，第19题8分，第20题8分，第21题9分，第22题10分，共55分)

16. 计算：(3.14-π)⁰+( $\text{[math]}$ )^-1+| $\text{[math]}$ |+2cos30°

查看解析收藏纠错

+选题
17. 先化简，后求值： $\text{[math]}$ ，其中，a是 $\text{[math]}$ 的小数部分(即，a= $\text{[math]}$ -2)．

查看解析收藏纠错

+选题
18. 为迎接义务教育均衡化检查，了解音乐课科目学生的学习情况，某校从八年级学生中抽取了部分学生进行了一次音乐素养测试，把测试结果分为四个等级：A级(优秀)，B级(良好)，C级(及格)，D级(不及格)，其中相应等级的得分依次为100分，80分，60分，40分，并将测试结果绘成了如图的两幅不完整的统计图，请根据统计图中的信息解答下列问题：

（1）本次抽样测试的学生人数是；

（2） A级在扇形统计图中对应的圆心角度数是 ▲ °，并把条形统计图补充完整；

（3）该校八年级有学生700名，若全部参加这次音乐素养测试，则估计不及格的人数为；

（4）这次抽测成绩的中位数是分；众数是分．

查看解析收藏纠错

+选题
19. 程大位是明代商人、珠算发明家在其杰作《算法统宗》(如图)中记载有如下问题：“以绳测井，若将绳三折测之，绳多五尺；若将绳四折测之，绳多一尺，绳长、井深各几何？”

译文：“用绳子测量水井的深度，如果将绳子折成三等份，一份绳子比井深多5尺；如果将绳子折成四等份，一份绳子比井深多1尺．绳长、井深各是多少尺？

（1）请你求出上述问题的解；

（2）若在(1)中的井底有一只青蛙，青蛙在井底想要爬出井外．第一天向上爬m尺；第二天休息，下滑2尺；第三天向上再爬m尺：第四天休息，下滑2尺……这只青蛙按照这样的规律向上爬与休息，若它想要在9天内(包括第9天)爬出井外，求m至少要为多少尺？

查看解析收藏纠错

+选题
20. 如图，AB是⊙O的直径，点P是射线AB上的一动点(不与点A，B重合)，过点P作⊙O的割线交⊙O于点C，D，BH⊥CD于H，连接BC，BD．

（1） ①在图1的情形下，证明：BC·BD=AB·BH ；
②当点P处于图2中的位置时，①中的结论 ▲ (填“仍成立”或“不再成立”)；

（2）若⊙O的半径为3，当∠APC=30°且BC·BD=6时，求AP的长．

查看解析收藏纠错

+选题

21. 如图，甲、乙分别从A(-9，0)，B(13，0)两点同时出发，甲朝着正北方向，以每秒3个单位长度的速度运动；乙朝着正西方向，以每秒4个单位长度的速度运动．设运动时间为t秒．

规定：t秒时，甲到达的位置记为点A，乙到达的位置记为点B，例如，1秒时，甲到达的位置记为A，乙到达的位置记为B，(如图所示)；2.5秒时，甲到达的位置记为A_2.5等等．容易知道，两条平行且相等的线段，其中包含有相同的方位信息所以，在研究有关运动问题时，为研究方便，我们可把点或线段进行合适的平移后，再去研究(物理上的相对运动观，就是源于这种数学方法)现对t秒时，甲、乙到达的位置点A_t ， B_t ，按如下步骤操作：

第一步：连接A_tB_t；

第二步：把线段A_tB_t进行平移，使点B_t与点B重合，平移后，点A₁的对应点用点A_t^’标记

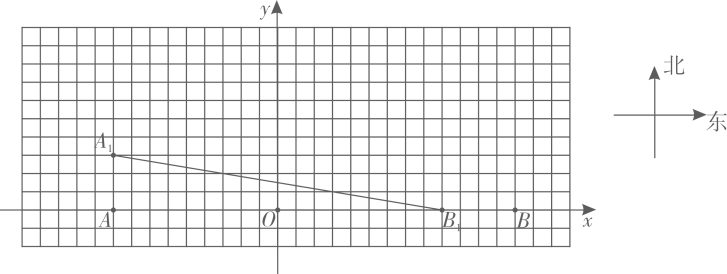
解答下列问题：

（1） [理解与初步应用]
当t=1时，

①利用网格，在上图中画出A₁ ， B₁经过上述第二步操作后的图形；

②此时，甲在乙的什么方位？(请填空)

答：此时，甲在乙的北偏西θ°(其中tanθ°= ，两者相距个单位长度．

（2） [实验与数据整理]
补全下表：

t的取值	1	2	3	t
点A_t'的坐标	(-5，3)	( ， )	( ， )	( ， )

（3） [数据分析与结论运用]

①如果把点A_t'的横、纵坐标分别用变量x，y表示，则y与x之间的函数关系式为；

②点A_3.5’的坐标为

（4） [拓展应用]
我们知道，在运动过程中的任意时刻t，甲相对于乙的方位(即，点A_t相对于点B_t的方位)与A_t'相对于点B的方位相同．这为我们解决某些问题，提供了新思路．

请解答：运动过程中，甲、乙之间的最近距离为个单位长度．

查看解析收藏纠错

+选题

22. 如图，四边形ABCD中，AB=6，CD=9，∠ABC+∠DCB=120°，点P是对角线AC上的一动点(不与点A，C重合)，过点P作PE∥CD，PF∥AB，分别交AD，BC于点E，F，连接EF．

（1）求∠EPF的度数；

（2）设PE=x，PF=y，随着点P的运动，x+ $\text{[math]}$ y的值是否会发生变化？若变化，请求出它的变化范围；若不变，请求出它的值；

（3）求EF的取值范围(可直接写出最后结果) ．

查看解析收藏纠错

+选题

广东省深圳市福田区八校2022-2023学年九年级5月质量检测联考数学试题

一、选择题：(每小题只有一个选项正确，每小题3分，共计30分)

二、填空题：(本大题共5小题，每小题3分，共15分)

三、解答题：(本题共7小题，其中第16题6分，第17题6分，第18题8分，第19题8分，第20题8分，第21题9分，第22题10分，共55分)

相关试卷 收起∨

相关试卷收起∨