冲刺2023中考——数学模拟考场仿真演练卷四

1. 我国神舟十三号载人飞船和航天员乘组于2022年4月16日返回地球，结束了183天的在轨飞行时间．从2003年神舟五号载人飞船上天以来，我国已有13位航天员出征太空，绕地球飞行共约2.32亿公里．将数据232000000用科学记数法表示为（）

A . 0.232×10⁹ B . 2.32×10⁹ C . 2.32×10⁸ D . 23.2×10⁸

查看解析收藏纠错

+选题
2. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，已知骰子相对两面的点数之和为7，下列图形为该骰子表面展开图的是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（）

A . ①②③ B . ①②④ C . ①③④ D . ②③④

查看解析收藏纠错

+选题
5. 射击比赛中，某队员的10次射击成绩如图所示，则下列结论错误的是（）

A . 平均数是9环 B . 中位数是9环 C . 众数是9环 D . 方差是0.8

查看解析收藏纠错

+选题
6. 如图1，在菱形ABCD中，∠C＝120°，M是AB的中点，N是对角线BD上一动点，设DN长为x，线段MN与AN长度的和为y，图2是y关于x的函数图象，图象右端点F的坐标为 $\text{[math]}$ ，则图象最低点E的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 在平面直角坐标系中，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，将 $\text{[math]}$ 绕 $\text{[math]}$ 点逆时针旋转到如图 $\text{[math]}$ 的位置， $\text{[math]}$ 的对应点 $\text{[math]}$ 恰好落在直线 $\text{[math]}$ 上，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，在平面直角坐标系中， $\text{[math]}$ 为 $\text{[math]}$ 的 $\text{[math]}$ 边上一点， $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 两点纵坐标分别为1、3，则 $\text{[math]}$ 点的纵坐标为（）

A . 4 B . 5 C . 6 D . 7

查看解析收藏纠错

+选题
9. 二次函数y＝ax²+bx+c的图象如图所示，则一次函数y＝bx+c和反比例函数y＝ $\text{[math]}$ 在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
10. 如图，在平面直角坐标系中，矩形ABCD的顶点A在第一象限，B，D分别在y轴上，AB交x轴于点E， $\text{[math]}$ 轴，垂足为F．若 $\text{[math]}$ ， $\text{[math]}$ ．以下结论正确的个数是（）
① $\text{[math]}$ ；②AE平分 $\text{[math]}$ ；③点C的坐标为 $\text{[math]}$ ；④ $\text{[math]}$ ；⑤矩形ABCD的面积为 $\text{[math]}$ ．

A . 2个 B . 3个 C . 4个 D . 5个

查看解析收藏纠错

+选题

11. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
12. 如图，点A，C，D，B在⊙O上，AC＝BC，∠ACB＝90°．若CD＝a，tan∠CBD＝ $\text{[math]}$ ，则AD的长是．

查看解析收藏纠错

+选题
13. 已知关于x的方程 $\text{[math]}$ 的解为负数，则a的取值范围是．

查看解析收藏纠错

+选题
14. 为了比较甲、乙两鱼池中的鱼苗数目，小明从两鱼池中各捞出100条鱼苗，每条做好记号，然后放回原鱼池；一段时间后，在同样的地方，小明再从甲、乙两鱼池中各捞出100条鱼苗，发现其中有记号的鱼苗分别是5条、10条，可以初步估计鱼苗数目较多的是鱼池（填甲或乙）

查看解析收藏纠错

+选题
15. 已知二次函数 $\text{[math]}$ ，图象的一部分如图所示，该函数图象经过点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ .对于下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ （其中 $\text{[math]}$ ）；⑤若 $\text{[math]}$ 和 $\text{[math]}$ 均在该函数图象上，且 $\text{[math]}$ ，则 $\text{[math]}$ .其中正确结论的个数共有个.

查看解析收藏纠错

+选题
16. 如图，在平面直角坐标系中， $\text{[math]}$ 斜边上的高为1， $\text{[math]}$ ，将 $\text{[math]}$ 绕原点顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，点A的对应点C恰好在函数 $\text{[math]}$ 的图象上，若在 $\text{[math]}$ 的图象上另有一点M使得 $\text{[math]}$ ，则点M的坐标为.

查看解析收藏纠错

+选题

17.

（1）解不等式组 $\text{[math]}$ ，并写出该不等式组的最小整数解．

（2）先化简，再求值：（ $\text{[math]}$ +1）÷ $\text{[math]}$ ，其中a＝4sin30°﹣（π﹣3）⁰ ．

查看解析收藏纠错

+选题
18. 八年级课外兴趣小组活动时，老师提出了如下问题：
将 $\text{[math]}$ 因式分解．
【观察】经过小组合作交流，小明得到了如下的解决方法：
解法一：原式 $\text{[math]}$
解法二：原式 $\text{[math]}$
【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）

（1）【类比】
请用分组分解法将 $\text{[math]}$ 因式分解；

（2）【挑战】
请用分组分解法将 $\text{[math]}$ 因式分解；

（3）【应用】
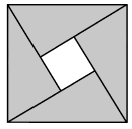
“赵爽弦图”是我国古代数学的骄傲，我们利用它验证了勾股定理．如图，“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形．若直角三角形的两条直角边长分别是a和 $\text{[math]}$ ，斜边长是3，小正方形的面积是1．根据以上信息，先将 $\text{[math]}$ 因式分解，再求值．

查看解析收藏纠错

+选题
19. 某中学为了解学生每学期诵读经典的情况，在全校范围内随机抽查了部分学生上一学期阅读量，学校将阅读量分成优秀、良好、较好、一般四个等级，绘制如下统计表：
等级
一般
较好
良好
优秀
阅读量/本
3
4
5
6
频数
12
a
14
4
频率
0.24
0.40
b
c
请根据统计表中提供的信息，解答下列问题：

（1）本次调查一共随机抽取了名学生；表中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

（2）求所抽查学生阅读量的众数和平均数．

（3）样本数据中优秀等级学生有4人，其中仅有1名男生．现从中任选派2名学生去参加读书分享会，请用树状图法或列表法求所选2名同学中有男生的概率

查看解析收藏纠错

+选题
20. 如图，AB是半圆O的直径，点C在半圆O上，点D为 $\text{[math]}$ 的中点，连接AC，BC，AD，AD与BC相交于点G，过点D作直线DE $\text{[math]}$ BC，交AC的延长线于点E．

（1）求证：DE是⊙O的切线；

（2）若 $\text{[math]}$ ， CG＝2 $\text{[math]}$ ，求阴影部分的面积．

查看解析收藏纠错

+选题
21. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情．如图是某滑雪场的横截面示意图，雪道分为AB，BC两部分，小明同学在C点测得雪道BC的坡度i=1：2.4，在A点测得B点的俯角∠DAB=30°．若雪道AB长为270m，雪道BC长为260m．

（1）求该滑雪场的高度h；

（2）据了解，该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求，其中甲设备每小时造雪量比乙设备少35m³ ，且甲设备造雪150m³所用的时间与乙设备造雪500m³所用的时间相等．求甲、乙两种设备每小时的造雪量．

查看解析收藏纠错

+选题
22. 如图，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 边上的高 $\text{[math]}$ ，点E为 $\text{[math]}$ 边上的动点（不与B、C重合，过点E作直线 $\text{[math]}$ 的垂线，垂足为F，连接 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ；

（2）当点E为 $\text{[math]}$ 的中点时，求 $\text{[math]}$ 的长；

（3）设 $\text{[math]}$ 的面积为y，求y与x之间的函数关系式，并求当x为何值时，y有最大值，最大值是多少？

查看解析收藏纠错

+选题
23. 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 和点 $\text{[math]}$ ．

（1）求一次函数的表达式；

（2）结合图象，写出当 $\text{[math]}$ 时，满足 $\text{[math]}$ 的x的取值范围；

（3）将一次函数的图象平移，使其经过坐标原点．直接写出一个反比例函数表达式，使它的图像与平移后的一次函数图象无交点．

查看解析收藏纠错

+选题
24. 如图，在平面直角坐标系中，经过点 $\text{[math]}$ 的直线AB与y轴交于点 $\text{[math]}$ ．经过原点O的抛物线 $\text{[math]}$ 交直线AB于点A，C，抛物线的顶点为D．

（1）求抛物线 $\text{[math]}$ 的表达式；

（2） M是线段AB上一点，N是抛物线上一点，当 $\text{[math]}$ 轴且 $\text{[math]}$ 时，求点M的坐标；

（3） P是抛物线上一动点，Q是平面直角坐标系内一点．是否存在以点A，C，P，Q为顶点的四边形是矩形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

冲刺2023中考——数学模拟考场仿真演练卷四

一、单选题（每题3分，共30分）

二、填空题（每空3分，共18分）

三、解答题（共8题，共72分）

相关试卷收起∨

等级	一般	较好	良好	优秀
阅读量/本	3	4	5	6
频数	12	a	14	4
频率	0.24	0.40	b	c

冲刺2023中考——数学模拟考场仿真演练卷四

一、单选题（每题3分，共30分）

二、填空题（每空3分，共18分）

三、解答题（共8题，共72分）

相关试卷 收起∨

相关试卷收起∨