2023年浙教版数学八年级下册第五章特殊平行四边形单元测试（进阶版）

1. 如图，在矩形ABCD中，AD＝3，AB＝4，M为线段BD上一动点，MP⊥CD于点P，MQ⊥BC于点Q，则PQ的最小值为（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，矩形ABCD中，AB＝2，BC＝3，P是CD边的中点，E是BC边上的一动点，M、N分别是AE、PE的中点，随着点E的运动，线段MN长（）

A . 不断增大 B . 先增大，后减小 C . 保持不变，长度为 $\text{[math]}$ D . 保持不变，长度为 $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，正方形纸片ABCD的四个顶点分别在四条平行线l₁、l₂、l₃、l₄上，这四条直线中相邻两条之间的距离依次为h₁、h₂、h₃（h₁＞0，h₂＞0，h₃＞0），若h₁＝5，h₂＝2，则正方形ABCD的面积S等于（）

A . 34 B . 89 C . 74 D . 109

查看解析收藏纠错

+选题
4. 如图，在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，对角线AC，BD交于点O，AC平分 $\text{[math]}$ ，过点C作 $\text{[math]}$ 交AB的延长线与点E，连接OE．
嘉嘉说：“四边形ABCD是菱形．”
琪琪说：“ $\text{[math]}$ ． ”
对于他俩的说法，正确的是（）

A . 嘉嘉正确，琪琪错误 B . 嘉嘉错误，琪琪正确 C . 他俩都正确 D . 他俩都错误

查看解析收藏纠错

+选题
5. 如图，在菱形ABCD中，对角线AC与BD相交于点O ， $\text{[math]}$ ，点E、F分别是BC、CD的中点，BD分别与AE、AF相交于点M、N ，连接OE、OF、EF ，下列结论：① $\text{[math]}$ 是等边三角形；②四边形CEOF是菱形；③ $\text{[math]}$ ；④ $\text{[math]}$ ，其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
6. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示．连结CF，并延长交AB于点N．若AB＝3 $\text{[math]}$ ， EF＝3，则FN的长为（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . 3

查看解析收藏纠错

+选题
7. 如图，大正方形与小正方形的面积之差是50，则阴影部分的面积是（）

A . 12.5 B . 25 C . 50 D . 100

查看解析收藏纠错

+选题
8. 数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具，此时测得 $\text{[math]}$ ，对角线 $\text{[math]}$ 长为 $\text{[math]}$ ，改变教具的形状成为图2所示的正方形，则正方形的对角线长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E，F，G，H分别在矩形 $\text{[math]}$ 各边上，且四边形 $\text{[math]}$ 为平行四边形，则平行四边形 $\text{[math]}$ 周长的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，正方形 $\text{[math]}$ 中，点P为 $\text{[math]}$ 延长线上任一点，连结 $\text{[math]}$ ，过点P作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点E，过点E作 $\text{[math]}$ 于点F.下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④若 $\text{[math]}$ ，则 $\text{[math]}$ .其中正确的个数为（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

11. 如阳，在矩形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，若 $\text{[math]}$ cm， $\text{[math]}$ cm，则 $\text{[math]}$ cm．

查看解析收藏纠错

+选题
12. 如图，在矩形ABCD中，∠ACB=30°，BC=2 $\text{[math]}$ ，点E是边BC上一动点（点E不与B，C重合），连接AE，AE的中垂线FG分别交AE于点F，交AC于点G，连接DG，GE．设AG=a，则点G到BC边的距离为（用含a的代数式表示）， $\text{[math]}$ ADG的面积的最小值为．

查看解析收藏纠错

+选题
13. 如图，在线段AB上取一点C，分别以AC，BC为边长作菱形BCFG和菱形ACDE，使点D在边CF上，连接EG，H是EG的中点，且 $\text{[math]}$ ，则EG的长是．

查看解析收藏纠错

+选题
14. 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，过菱形 $\text{[math]}$ 的对称中心O分别作边 $\text{[math]}$ ， $\text{[math]}$ 的垂线，交各边于点E，F，G，H，则菱形 $\text{[math]}$ 的面积为，四边形 $\text{[math]}$ 的周长为．

查看解析收藏纠错

+选题
15. 把8个边长为1的正方形按如图所示摆放在直角坐标系中，经过原点O的直线l将这8个正方形分成面积相等的两部分，则该直线的函数表达式是．

查看解析收藏纠错

+选题
16. 菱形ABCD中，AD＝4，∠DAB＝60°，E、F、G、H分别是AD、AB、BC、CD上的点，且DH＝FB ， DE＝BG ，当四边形EFGH为正方形时，DH＝．

查看解析收藏纠错

+选题

17. 定义：有一组邻边垂直且对角线相等的四边形为垂等四边形.

（1）写出一个已学的特殊平行四边形中是垂等四边形的是.

（2）如图1，在3×3方格纸中，A，B，C在格点上，请画出两个符合条件的不全等的垂等四边形，使AC，BD是对角线，点D在格点上.

（3）如图2，在正方形ABCD中，点E，F，G分别在AD，AB，BC上，AE＝AF＝CG且∠DGC＝∠DEG，求证：四边形DEFG是垂等四边形.

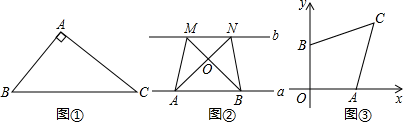
（4）如图3，已知Rt△ABC，∠B＝90°，∠C＝30°，AB＝2，以AC为边在AC的右上方作等腰三角形，使四边形ABCD是垂等四边形，请直接写出四边形ABCD的面积.

查看解析收藏纠错

+选题
18. 定义：数学活动课上，陈老师给出如下定义：有一组对边相等而另一组对边不相等的凸四边形叫做它的对等四边形．

（1）在图1，图2中，点A、B、C都在格点(小正方形的顶点)上，请在图1，图2中各画一个以格点为顶点，AB、BC为边的一个对等四边形ABCD(两个图形不全等)；

（2）如图3，对等四边形ABCD中，∠ADC=90°，AB=BD=CD=10，AD=12，求BC的长．

查看解析收藏纠错

+选题

19. 如图，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 且分别交对角线 $\text{[math]}$ 于点E，F．

（1）求证： $\text{[math]}$ ；

（2）当四边形 $\text{[math]}$ 分别是矩形和菱形时，请分别说出四边形 $\text{[math]}$ 的形状，并说明理由．

查看解析收藏纠错

+选题
20. 如图1，在 $\text{[math]}$ 中，点D在BC的延长线上，点O是AC边上的一个动点，过点O作直线 $\text{[math]}$ ，设MN交 $\text{[math]}$ 的平分线于点E，交 $\text{[math]}$ 的平分线于点F ．

（1）线段CE与CF的位置关系是；

（2）探究：线段OE与OF的数量关系，并加以证明；

（3）如图2，连接AE ， AF ，当点O运动到何处时，四边形AECF是矩形，并说明理由；

（4）在（3）的前提下， $\text{[math]}$ 满足什么条件时，四边形AECF是正方形，请说明理由．

查看解析收藏纠错

+选题
21. 如图，在平面直角坐标系xOy中，直线AB： $\text{[math]}$ 与直线CD： $\text{[math]}$ 相交于点 $\text{[math]}$ ，分别交坐标轴于点A，B，C，D．

（1）求a和k的值；

（2）如图，点P是直线CD上的一个动点，当 $\text{[math]}$ 的面积为20时，求点P的坐标；

（3）直线AB上有一点F，在平面直角坐标系内找一点N，使得以BF为一边，以点B，D，F，N为顶点的四边形是菱形，请直接写出符合条件的点N的坐标．

查看解析收藏纠错

+选题
22. 定义：对角线相等的四边形称为对美四边形．

（1）我们学过的对美四边形有、．（写出两个）

（2）如图1，D为等腰△ABC底边AB上的一点，连结CD，过C作 $\text{[math]}$ ，以B为顶点作 $\text{[math]}$ 交CF于点E，求证：四边形CDBE为对美四边形．

（3）如图2，对美四边形ABCD中，对角线AC、BD交于点O，AC=BD， $\text{[math]}$ ．
①若 $\text{[math]}$ ， $\text{[math]}$ ，求四边形ABCD的面积．

②若 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ ，试求出y与x的关系式．

查看解析收藏纠错

+选题
23. 如图1，矩形ABCD中，过对角线AC的中点O画EF⊥AC分别交AB，CD于点E，F，连结AF，CE．

（1） [证明体验]
求证：四边形AECF是菱形．

（2） [基础巩固]
若AB=8，BC=6，求菱形AECF的边长．

（3） [拓展延伸]
如图2，在对角线AC上取点G，H，使得四边形EHFG是正方形，若正方形EHFG的边长为 $\text{[math]}$ ，且AE=5CH，求矩形ABCD的面积．

查看解析收藏纠错

+选题
24. 问题提出

（1）如图①，在Rt△ABC中，∠A＝90°，AB＝3，AC＝4，在BC上找一点D，使得AD将△ABC分成面积相等的两部分，作出线段AD，并求出AD的长度；
问题探究

（2）如图②，点A、B在直线a上，点M、N在直线b上，且a∥b，连接AN、BM交于点O，连接AM、BN，试判断△AOM与△BON的面积关系，并说明你的理由；
解决问题

（3）如图③，刘老伯有一个形状为筝形OACB的养鸡场，在平面直角坐标系中，O（0，0）、A（4，0）、B（0，4）、C（6，6），是否在边AC上存在一点P，使得过B、P两点修一道笔直的墙（墙的宽度不计），将这个养鸡场分成面积相等的两部分？若存在，请求出直线BP的表达式；若不存在，请说明理由．

查看解析收藏纠错

+选题

2023年浙教版数学八年级下册第五章特殊平行四边形单元测试（进阶版）

一、单选题（每题3分，共30分）

二、填空题（每题3分，共21分）

三、作图题（共10分）

四、解答题（共6题，共51分）

相关试卷收起∨

2023年浙教版数学八年级下册第五章 特殊平行四边形 单元测试（进阶版）

一、单选题（每题3分，共30分）

二、填空题（每题3分，共21分）

三、作图题（共10分）

四、解答题（共6题，共51分）

相关试卷 收起∨

2023年浙教版数学八年级下册第五章特殊平行四边形单元测试（进阶版）

相关试卷收起∨