浙江省金华市2022年中考数学试卷

1. 在 -2、 $\text{[math]}$ 、 $\text{[math]}$ 、2中，是无理数的是（）

A . -2 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
2. 计算 a³·a² 的结果是（）

A . a B . a⁶ C . 6a D . a⁵

查看解析收藏纠错

+选题
3. 体现我国先进核电技术的“华龙一号”，年发电能力相当于减少二氧化碳排放16320000吨，数16320000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 已知三角形的两边长分别为5cm和8cm，则第三边的长可以是（）

A . 2cm B . 3cm C . 6cm D . 13cm

查看解析收藏纠错

+选题
5. 观察如图所示的频数直方图，其中组界为99.5~124.5这一组的频数为（）

A . 5 B . 6 C . 7 D . 8

查看解析收藏纠错

+选题
6. 如图，AC与BD相交于点O，OA=OD，OB=OC，不添加辅助线，判定△ABO≌△DCO的依据是（）

A . SSS B . SAS C . AAS D . HL

查看解析收藏纠错

+选题
7. 如图是城市某区域的示意图，建立平面直角坐标系后，学校和体育场的坐标分别是(3，1)，(4，-2)，下列各地点中，离原点最近的是（）

A . 超市 B . 医院 C . 体育场 D . 学校

查看解析收藏纠错

+选题
8. 如图，圆柱的底面直径为AB，高为AC.一只蚂蚁在C处，沿圆柱的侧面爬到B处，现将圆柱侧面沿AC“剪开”，在侧面展开图上画出蚂蚁爬行的最近路线，正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
9. 一配电房示意图如图所示，它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图是一张矩形纸片ABCD，点E为AD中点，点F在BC上，把该纸片沿EF折叠，点A，B的对应点分别为A'，B'，A'E与BC相交于点G，B'A'的延长线过点C，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 因式分解： $\text{[math]}$ =.

查看解析收藏纠错

+选题
12. 若分式 $\text{[math]}$ 的值为2，则x的值是.

查看解析收藏纠错

+选题
13. 一个布袋里装有7个红球、3白球，它们除颜色外都相同.从中任意摸出1个球，摸到红球的概率是.

查看解析收藏纠错

+选题
14. 如图，在Rt△ABC中， ∠ACB=90°，∠A=30°，BC=2cm .把 △ABC沿AB方向平移1cm，得到△A'B'C' ，连结CC'，则四边形AB'C'C 的周长为cm..

查看解析收藏纠错

+选题
15. 如图，木工用角尺的短边紧靠⊙О于点A，长边与⊙О相切于点B，角尺的直角顶点为C，已知AC=6cm，CB=8cm，则⊙О的半径为cm.

查看解析收藏纠错

+选题
16. 图1是光伏发电场景，其示意图如图2，EF为吸热塔，在地平线EG上的点B，B'处各安装定日镜(介绍见图3).绕各中心点(A，A')旋转镜面，使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1m，EB=8m，EB'=8 $\text{[math]}$ m，在点A观测点F的仰角为45°

（1）点F的高度EF为m.

（2）设∠DAB=α，∠D'A'B'=β，则α与β的数量关系是.

查看解析收藏纠错

+选题

17. 计算 $\text{[math]}$

查看解析收藏纠错

+选题
18. 解不等式：2(3x-2)>x+1.

查看解析收藏纠错

+选题
19. 如图1，将长为2a+3，宽为2a的矩形分割成四个全等的直角三角形，拼成“赵爽弦图”(如图2)，得到大小两个正方形，

（1）用关于a的代数式表示图2中小正方形的边长

（2）当a=3时，该小正方形的面积是多少？

查看解析收藏纠错

+选题
20. 如图，点A在第一象限内，AB⊥x轴于点B，反比例函数 $\text{[math]}$ 的图象分别交AO，AB于点C，D.已知点C的坐标为(2，2)，BD=1.

（1）求k的值及点D的坐标.

（2）已知点P在该反比例函数图象上，且在△ABO的内部（包括边界），直接写出点P的横坐标x的取值范围.

查看解析收藏纠错

+选题

21. 学校举办演讲比赛，总评成绩由“内容、表达、风度、印象”四部分组成。九(1)班组织选拔赛，制定的各部分所占比例如下图，三位同学的成绩如下表.请解答下列问题：

演讲总评成绩各部分所占比例的统计图

三位同学的成绩统计表

	内容	表达	风度	印象	总评成绩
小明	8	7	8	8	m
小亮	7	8	8	9	7.85
小田	7	9	7	7	7.8

（1）求图中表示“内容”的扇形的圆心角度数.

（2）求表中m的值，并根据总评成绩确定三人的排名顺序.

（3）学校要求“内容”比“表达”重要，该统计图中各部分所占比例是否合理？如果不合理，如何调整？

查看解析收藏纠错

+选题

22. 如图

如图1，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答下列问题：

作法如图2.

1.作直径AF.

2.以F为圆心，FO为半径作圆弧，与⊙O交于点M，N.

3.连结AM，MN，NA.

（1）求∠ABC的度数.

（2） △AMN是正三角形吗？请说明理由.

（3）从点A开始，以DN长为半径，在⊙O上依次截取点，再依次连结这些分点，得到正n边形，求n的值.

查看解析收藏纠错

+选题

23. “八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：

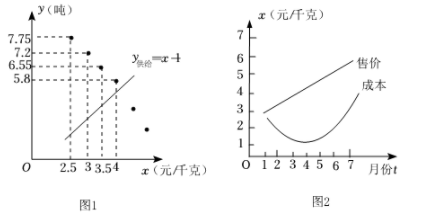
①统计售价与需求量的数据，通过描点(图1)，发现该蔬菜需求量y_需求(吨)关于售价x(元/千克)的函数图象可以看成抛物线，其表达式为 $\text{[math]}$ ，部分对应值如下表：

售价x(元/千克)	…	2.5	3	3.5	4	…
需求量y_需求(吨）	…	7.75	7.2	6.55	5.8	…

②该蔬菜供给量y_供给(吨)关于售价x(元/千克)的函数表达式为y_供给=x-1，函数图象见图1.

③1~7月份该蔬菜售价x_售价(元/千克)、成本x_成本(元/千克)关于月份t的函数表达式分别为 $\text{[math]}$ ， $\text{[math]}$ ，函数图象见图2.

请解答下列问题：

（1）求a，c的值.

（2）根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由.

（3）求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润.

查看解析收藏纠错

+选题

24. 如图，在菱形ABCD中，AB=10. $\text{[math]}$ ，点E从点B出发沿折线B-C-D向终点D运动.过点E作点E所在的边(BC或CD)的垂线，交菱形其它的边于点F，在EF的右侧作矩形EFGH.

（1）如图1，点G在AC上.求证：FA=FG.

（2）若EF=FG，当EF过AC中点时，求AG的长.

（3）已知FG=8，设点E的运动路程为s.当s满足什么条件时，以G，C，H为顶点的三角形与△BEF相似(包括全等)？

查看解析收藏纠错

+选题

浙江省金华市2022年中考数学试卷

一、选择题(本题有10小题，每小题3分，共30分)

二、填空题(本题有6小题，每小题4分，共24分)

三、解答题(本题有8小题，共66分，)

相关试卷收起∨

浙江省金华市2022年中考数学试卷

一、选择题(本题有10小题，每小题3分，共30分)

二、填空题(本题有6小题，每小题4分，共24分)

三、解答题(本题有8小题，共66分，)

相关试卷 收起∨

相关试卷收起∨