四川省自贡市2022年中考数学试卷

修改时间：2024-07-13 浏览次数：171 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题（共12个小题，每小题4分，共48分）

1. 如图，直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ；若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 30° B . 40° C . 60° D . 150°

查看解析收藏纠错

+选题
2. 自贡市江姐故里红色教育基地自去年底开放以来，截止今年5月，共接待游客180000余人；人数180000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，将矩形纸片ABCD 绕边CD所在的直线旋转一周，得到的立体图形是（ )

A . B . C . D .

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 如图，菱形 ABCD 对角线交点与坐标原点 O 重合，点 A（-2，5），则点C的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 剪纸与扎染、龚扇被称为自贡小三绝，以下学生剪纸作品中，轴对称图形是（）

A . ， B . C . D .

查看解析收藏纠错

+选题
7. 如图，四边形 $\text{[math]}$ 内接于⊙ $\text{[math]}$ ， $\text{[math]}$ 为⊙ $\text{[math]}$ 的直径， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 90° B . 100° C . 110° D . 120°

查看解析收藏纠错

+选题
8. 六位同学的年龄分别是13、14、15、14、14、15岁，关于这组数据，正确说法是（）

A . 平均数是14 B . 中位数是14.5 C . 方差3 D . 众数是14

查看解析收藏纠错

+选题
9. 等腰三角形顶角度数比一个底角度数的2倍多20°，则这个底角的度数为（）

A . 30° B . 40° C . 50° D . 60°

查看解析收藏纠错

+选题
10. $\text{[math]}$ 为⊙ $\text{[math]}$ 外一点， $\text{[math]}$ 与⊙ $\text{[math]}$ 相切于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 5 C . 8 D . 9

查看解析收藏纠错

+选题
11. 九年级2班计划在劳动实践基地内种植蔬菜，班长买回来8米长的围栏，准备围成一边靠墙（墙足够长）的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形，等腰三角形（底边靠墙），半圆形这三种方案，最佳方案是（）

A . 方案1 B . 方案2 C . 方案3 D . 方案1或方案2

查看解析收藏纠错

+选题
12. 已知 $\text{[math]}$ ，抛物线 $\text{[math]}$ 顶点在线段 $\text{[math]}$ 上运动，形状保持不变，与 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点（ $\text{[math]}$ 在 $\text{[math]}$ 的右侧），下列结论：
①. $\text{[math]}$ ；②.当 $\text{[math]}$ 时，一定有 $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大；③.若点 $\text{[math]}$ 横坐标的最小值为-5，点 $\text{[math]}$ 横坐标的最大值为3；④.当四边形 $\text{[math]}$ 为平行四边形时， $\text{[math]}$ .

其中正确的是（）

A . ①③ B . ②③ C . ①④ D . ①③④

查看解析收藏纠错

+选题

二、填空题（共6个小题，每小题4分，共24分）

13. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 分解因式： $\text{[math]}$ ．

查看解析收藏纠错

+选题
15. 化简： $\text{[math]}$ = .

查看解析收藏纠错

+选题
16. 为了比较甲、乙两鱼池中的鱼苗数目，小明从两鱼池中各捞出100条鱼苗，每条做好记号，然后放回原鱼池；一段时间后，在同样的地方，小明再从甲、乙两鱼池中各捞出100条鱼苗，发现其中有记号的鱼苗分别是5条、10条，可以初步估计鱼苗数目较多的是鱼池（填甲或乙）

查看解析收藏纠错

+选题
17. 一块圆形玻璃镜面碎成了几块，其中一块如图所示，测得弦 $\text{[math]}$ 长20厘米，弓形高 $\text{[math]}$ 为2厘米，则镜面半径为厘米.

查看解析收藏纠错

+选题
18. 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，线段 $\text{[math]}$ 在边 $\text{[math]}$ 上左右滑动；若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为 .

查看解析收藏纠错

+选题

三、解答题（共8个题，共78分）

19. 解不等式组： $\text{[math]}$ ，并在数轴上表示其解集.

查看解析收藏纠错

+选题
20. 如图，△ $\text{[math]}$ 是等边三角形， $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ .

求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
21. 学校师生去距学校45千米的吴玉章故居开展研学活动，骑行爱好者张老师骑自行车先行2小时后，其余师生乘汽车出发，结果同时到达；已知汽车速度是自行车速度的3倍，求张老师骑车的速度.

查看解析收藏纠错

+选题
22. 为了解学生每周参加课外兴趣小组活动的累计时间 $\text{[math]}$ （单位：小时），学校采用随机抽样的方法，对部分学生进行了问卷调查，调查结果按 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分为四个等级，分别用A、B、C、D表示；下图是受损的调查统计图，请根据图上残存信息解决以下问题：

（1）求参与问卷调查的学生人数 $\text{[math]}$ ，并将条形统计图补充完整；

（2）全校共有学生2000人，试估计学校每周参加课外兴趣小组活动累计时间不少于4小时的学生人数；

（3）某小组有4名同学，A、D等级各2人，从中任选2人向老师汇报兴趣活动情况，请用画树状图或列表法求这2人均属D等级的概率.

查看解析收藏纠错

+选题
23. 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ 两点.

（1）求反比例函数和一次函数的解析式；

（2）过点 $\text{[math]}$ 作直线 $\text{[math]}$ ∥ $\text{[math]}$ 轴，过点 $\text{[math]}$ 作直线 $\text{[math]}$ 于 $\text{[math]}$ ，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上一动点，若 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标.

查看解析收藏纠错

+选题
24. 如图，用四根木条钉成矩形框 $\text{[math]}$ ，把边 $\text{[math]}$ 固定在地面上，向右推动矩形框，矩形框的形状会发生改变（四边形具有不稳定性）.

（1）通过观察分析，我们发现图中线段存在等量关系，如线段 $\text{[math]}$ 由 $\text{[math]}$ 旋转得到，所以 $\text{[math]}$ .我们还可以得到 $\text{[math]}$ = ， $\text{[math]}$ = ；

（2）进一步观察，我们还会发现 $\text{[math]}$ ∥ $\text{[math]}$ ，请证明这一结论；

（3）已知 $\text{[math]}$ ，若 $\text{[math]}$ 恰好经过原矩形 $\text{[math]}$ 边的中点 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 之间的距离.

查看解析收藏纠错

+选题
25. 某数学兴趣小组自制测角仪到公园进行实地测量，活动过程如下：

（1）探究原理制作测角仪时，将细线一段固定在量角器圆心 $\text{[math]}$ 处，另一端系小重物 $\text{[math]}$ .测量时，使支杆 $\text{[math]}$ 、量角器90°刻度线 $\text{[math]}$ 与铅垂线 $\text{[math]}$ 相互重合（如图①），绕点 $\text{[math]}$ 转动量角器，使观测目标 $\text{[math]}$ 与直径两端点 $\text{[math]}$ 共线（如图②），此目标 $\text{[math]}$ 的仰角 $\text{[math]}$ .请说明两个角相等的理由.

（2）实地测量
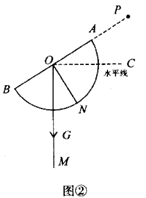
如图③，公园广场上有一棵树，为了测量树高，同学们在观测点 $\text{[math]}$ 处测得顶端 $\text{[math]}$ 的仰角 $\text{[math]}$ ，观测点与树的距离 $\text{[math]}$ 为5米，点 $\text{[math]}$ 到地面的距离 $\text{[math]}$ 为1.5米；求树高 $\text{[math]}$ . （ $\text{[math]}$ ，结果精确到0.1米）

（3）拓展探究
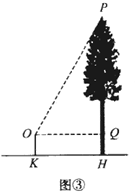
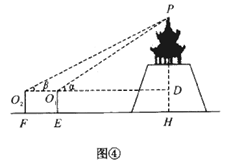
公园高台上有一凉亭，为测量凉亭顶端 $\text{[math]}$ 距离地面高度 $\text{[math]}$ （如图④），同学们讨论，决定先在水平地面上选取观测点 $\text{[math]}$ （ $\text{[math]}$ 在同一直线上），分别测得点 $\text{[math]}$ 的仰角 $\text{[math]}$ ，再测得 $\text{[math]}$ 间的距离 $\text{[math]}$ ，点 $\text{[math]}$ 到地面的距离 $\text{[math]}$ 均为1.5米；求 $\text{[math]}$ （用 $\text{[math]}$ 表示）.

查看解析收藏纠错

+选题
26. 已知二次函数 $\text{[math]}$ .

（1）若 $\text{[math]}$ ，且函数图象经过 $\text{[math]}$ ， $\text{[math]}$ 两点，求此二次函数的解析式，直接写出抛物线与 $\text{[math]}$ 轴交点及顶点的坐标；

（2）在图①中画出⑴中函数的大致图象，并根据图象写出函数值 $\text{[math]}$ 时自变量 $\text{[math]}$ 的取值范围；

（3）若 $\text{[math]}$ 且 $\text{[math]}$ ，一元二次方程 $\text{[math]}$ 两根之差等于 $\text{[math]}$ ，函数图象经过 $\text{[math]}$ 两点，试比较 $\text{[math]}$ 的大小 .

查看解析收藏纠错

+选题

四川省自贡市2022年中考数学试卷

一、选择题（共12个小题，每小题4分，共48分）

二、填空题（共6个小题，每小题4分，共24分）

三、解答题（共8个题，共78分）

相关试卷 收起∨

相关试卷收起∨