备考2022年中考数学一轮复习（湘教版）专题52 命题与证明

1. 下列命题是假命题的是（）

A . 任意一个三角形中，三角形两边的差小于第三边 B . 三角形的中位线平行于三角形的第三边，并且等于第三边的一半 C . 如果一个角的两边分别平行于另一个角的两边，那么这两个角一定相等 D . 一组对边平行且相等的四边形是平行四边形

查看解析收藏纠错

+选题
2. 下列命题中，为真命题的是（）
（1）对角线互相平分的四边形是平行四边形（2）对角线互相垂直的四边形是菱形（3）对角线相等的平行四边形是菱形（4）有一个角是直角的平行四边形是矩形

A . （1）（2） B . （1）（4） C . （2）（4） D . （3）（4）

查看解析收藏纠错

+选题
3. 以下四个命题：①任意三角形的一条中位线与第三边上的中线互相平分；②A ， B ， C ， D ， E ， F六个足球队进行单循环赛，若A ， B ， C ， D ， E分别赛了5，4，3，2，1场，则由此可知，还没有与B队比赛的球队可能是D队；③两个正六边形一定位似；④有13人参加捐款，其中小王的捐款数比13人捐款的平均数多2元，则小王的捐款数不可能最少，但可能只比最少的多．比其他的都少．其中真命题的个数有（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
4. 下列命题正确的是（　　）

A . 在函数 $\text{[math]}$ 中，当 $\text{[math]}$ 时，y随x的增大而减小 B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 垂直于半径的直线是圆的切线 D . 各边相等的圆内接四边形是正方形

查看解析收藏纠错

+选题
5. 定理：三角形的一个外角等于与它不相邻的两个内角的和．
已知：如图， $\text{[math]}$ 是 $\text{[math]}$ 的外角．

求证： $\text{[math]}$ ．

下列说法正确的是（）

A . 证法1还需证明其他形状的三角形，该定理的证明才完整 B . 证法1用严谨的推理证明了该定理 C . 证法2用特殊到一般法证明了该定理 D . 证法2只要测量够一百个三角形进行验证，就能证明该定理

查看解析收藏纠错

+选题
6. 下列命题中，真命题是（）

A . 若a＞b，则c﹣a＜c﹣b B . 某种彩票中奖的概率是1%，买100张该种彩票一定会中奖 C . 点M（x₁ ， y₁），点N（x₂ ， y₂）都在反比例函数y= $\text{[math]}$ 的图象上，若x₁＜x₂ ，则y₁＞y₂ D . 甲、乙两射击运动员分别射击10次，他们射击成绩的方差分别为 $\text{[math]}$ =4， $\text{[math]}$ =9，这过程中乙发挥比甲更稳定

查看解析收藏纠错

+选题
7. 现有下列命题：
①若 $\text{[math]}$ ，则一元二次方程 $\text{[math]}$ 有实数根；②有两条边长比值是 $\text{[math]}$ 的两个直角三角形相似；③有一条对角线平分一组对角的四边形是菱形；④若点 $\text{[math]}$ ， $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，且 $\text{[math]}$ ，则a的取值范围是 $\text{[math]}$ ．

其中真命题的个数为（）

A . 3个 B . 2个 C . 1个 D . 0个

查看解析收藏纠错

+选题
8. 下列命题的逆命题是真命题的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 同位角相等，两直线平行 C . 对顶角相等 D . 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$

查看解析收藏纠错

+选题

9. 下列说法错误的是（只填序号）
① $\text{[math]}$ 的整数部分为2，小数部分为 $\text{[math]}$ ．

②外角为 $\text{[math]}$ 且边长为2的正多边形的内切圆的半径为 $\text{[math]}$ ．

③把直线 $\text{[math]}$ 向左平移1个单位后得到的直线解析式为 $\text{[math]}$ ．

④新定义运算： $\text{[math]}$ ，则方程 $\text{[math]}$ 有两个不相等的实数根．

查看解析收藏纠错

+选题
10. 数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是（只填写序号）．
①射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；

②车轮做成圆形，应用了“圆是中心对称图形”；

③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；

④地板砖可以做成矩形，应用了“矩形对边相等”．

查看解析收藏纠错

+选题
11. “正方形对角线互相垂直平分”的逆命题是（填“真命题”或“假命题”）．

查看解析收藏纠错

+选题
12. 命题“如果 $\text{[math]}$ ，那么 $\text{[math]}$ ”，是（选填“真”或“假”）命题.

查看解析收藏纠错

+选题
13. 用一个 $\text{[math]}$ 的值推断命题“一次函数 $\text{[math]}$ 中， $\text{[math]}$ 随着 $\text{[math]}$ 的增大而增大．”是错误的，这个值可以是 $\text{[math]}$ =．

查看解析收藏纠错

+选题
14. 盒子里有甲、乙、丙三种粒子，若相同种类的两颗粒子发生碰撞，则变成一颗乙粒子；不同种类的两颗粒子发生碰撞，会变成第三种粒子，例如一颗甲粒子和一颗乙粒子发生碰撞则变成一颗丙粒子，现有甲粒子6颗，乙粒子4颗，丙粒子5颗，如果经过各种两两碰撞后，只剩下1颗粒子，给出下列结论：①最后一颗粒子可能是甲粒子；②最后一颗粒子一定不是乙粒子；③最后一颗粒子可能是丙粒子．其中正确结论的序号是：．

查看解析收藏纠错

+选题
15. “干支纪年法”是我国历法的一种传统纪年法，甲､乙､丙､丁､戊､已､庚､辛､壬､癸被称为“十天干”：子､丑､寅､卯､辰､已､午､未､申､酉､戍､亥叫做“十二地支”；“天干”以“甲”字开始，“地支”以“子”字开始，两者按干支顺序相配，组成了干支纪年法，其相配顺序为甲子､乙丑､丙寅…癸酉；甲戌､乙亥､丙子…癸未；甲申､乙酉､丙戌…癸已；…共得到60个组合，称六十甲子，周而复始，无穷无尽.2021年是“干支纪年法”中的辛丑年，那么2050年是“干支纪年法“中的.

查看解析收藏纠错

+选题
16. 判断命题“代数式 $\text{[math]}$ 的值一定大于代数式 $\text{[math]}$ 的值”是假命题，只需举出一个反例，反例中m的值为．

查看解析收藏纠错

+选题

17. 数学小组研究如下问题：长春市的纬度约为北纬 $\text{[math]}$ ，求北纬 $\text{[math]}$ 纬线的长度，小组成员查阅了相关资料，得到三条信息：
⑴在地球仪上，与南，北极距离相等的大圆圈，叫赤道，所有与赤道平行的圆圈叫纬线；

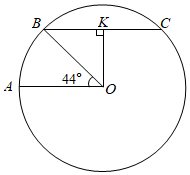
⑵如图， $\text{[math]}$ 是经过南、北极的圆，地球半径 $\text{[math]}$ 约为 $\text{[math]}$ ．弦 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则以 $\text{[math]}$ 为半径的圆的周长是北纬 $\text{[math]}$ 纬线的长度；

⑶参考数据： $\text{[math]}$ 取3， $\text{[math]}$ ， $\text{[math]}$ ．

小组成员给出了如下解答，请你补充完整：

解：因为 $\text{[math]}$ ， $\text{[math]}$ ，

所以 $\text{[math]}$ （        ）（填推理依据），

因为 $\text{[math]}$ ，所以 $\text{[math]}$ ，

在 $\text{[math]}$ 中， $\text{[math]}$ ．

$\text{[math]}$       ▲      （填“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）．

所以北纬 $\text{[math]}$ 的纬线长 $\text{[math]}$

$\text{[math]}$ ▲   （填相应的三角形函数值）

$\text{[math]}$    ▲   （ $\text{[math]}$ ）（结果取整数）．

查看解析收藏纠错

+选题
18. 证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半（要求：自己作图并写出已知、求证、证明）

查看解析收藏纠错

+选题

19. 今有甲、乙、丙三名候选人参与某村村长选举，共发出1800张选票，得票数最高者为当选人，且废票不计入任何一位候选人之得票数内，全村设有四个投开票所，目前第一、第二、第三投开票所已开完所有选票，剩下第四投开票所尚未开票，结果如表所示：
投开票所
候选人
废票
合计
甲
乙
丙
一
200
211
147
12
570
二
286
85
244
15
630
三
97
41
205
7
350
四

250
（单位：票）
请回答下列问题：

（1）请分别写出目前甲、乙、丙三名候选人的得票数；

（2）承（1），请分别判断甲、乙两名候选人是否还有机会当选村长，并详细解释或完整写出你的解题过程．

查看解析收藏纠错

+选题
20. 对于命题“相等的角是直角”，解决下列问题．

（1）指出命题的条件和结论，并改写成“如果…那么…”的形式；

（2）判断此命题是真命题还是假命题．

查看解析收藏纠错

+选题
21. 如图， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ ．

（1）填空：把下面的推理过程补充完整，并在括号内注明理由．
试说明： $\text{[math]}$ ．

解： $\text{[math]}$ ，

$\text{[math]}$      ▲    $\text{[math]}$   ▲   （       ）．

$\text{[math]}$ ，

即 $\text{[math]}$ ．

$\text{[math]}$     ▲    $\text{[math]}$     ▲   （         ）．

又 $\text{[math]}$ ，

$\text{[math]}$ （        ）．

（2）由（1）可得， $\text{[math]}$ 与 $\text{[math]}$ 平行吗？请说明理由，

查看解析收藏纠错

+选题

备考2022年中考数学一轮复习（湘教版）专题52 命题与证明

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

投开票所	候选人			废票	合计
投开票所	甲	乙	丙	废票	合计
一	200	211	147	12	570
二	286	85	244	15	630
三	97	41	205	7	350
四					250

备考2022年中考数学一轮复习（湘教版）专题52 命题与证明

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨