2015-2016学年黑龙江省哈尔滨市道里区九年级上学期期末数学试卷

1. 点A（﹣3，5）关于原点的对称点的坐标为（　　）

A . （3，5） B . （﹣3，﹣5） C . （3，﹣5） D . （5，﹣3）

查看解析收藏纠错

+选题
2. “珍惜生命，注意安全”是一永恒的话题．在现代化的城市，交通安全晚不能被忽视，下列几个图形是国际通用的几种交通标志，其中不是中心对称图形是（　　）

A . 禁止行车 B . 禁止行人通行 C . 禁止车辆长时间停放 D . 禁止车辆临时或长时间停放

查看解析收藏纠错

+选题
3. 在Rt△ABC中，∠C=90°，若sinA= $\text{[math]}$ ，则cosB的值是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 抛物线y=﹣5（x﹣2）²+3的顶点坐标是（　　）

A . （2，3） B . （﹣2，3） C . （2，﹣3） D . （﹣2，﹣3）

查看解析收藏纠错

+选题
5. 在反比例函数 y= $\text{[math]}$ 的图象的每一条曲线上，y都随x的增大而减小，则k的取值范围是（　　）

A . k＞1 B . k＞0 C . k≥1 D . k＜1

查看解析收藏纠错

+选题
6.
如图所示的几何体是由六个相同的小正方体组合而成的，它的俯视图是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
7. 如图，E是平行四边形ABCD的边BA延长线上的一点，CE交AD于点F，下列各式中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8.
如图，AB为⊙O的直径，弦CD⊥AB于点E，若AE=8，BE=2，则CD=（　　）

A . 6 B . 8 C . 2 $\text{[math]}$ D . 4 $\text{[math]}$

查看解析收藏纠错

+选题
9. 在函数y= $\text{[math]}$ （k＜0）的图象上有三点A_l（x_l ， y₁）、A₂（x₂ ， y₂）、A₃（x₃ ， y₃），已知x_l＜x₂＜0＜x₃ ，则下列各式正确的是（　　）

A . y₁＜y₂＜y₃ B . y₃＜y₂＜y₁ C . y₂＜y₁＜y₃ D . y₃＜y₁＜y₂

查看解析收藏纠错

+选题
10.
已知二次函数y=ax²+bx+c的图象如图所示，其对称轴为直线x=﹣1，给出下列结论：（1）b²＞4ac；（2）abc＞0；（3）2a+b=0；（4）a+b+c＞0；（5）a﹣b+c＜0．其中正确的结论有（　　）

A . 2个 B . 3个 C . 4个 D . 5个

查看解析收藏纠错

+选题

11. 在Rt△ABC中，∠C=90°，AC=1，AB=2，则sinA=

查看解析收藏纠错

+选题
12. 将二次函数y=x²+4x﹣2配方成y=（x﹣h）²+k的形式，则y= ．

查看解析收藏纠错

+选题
13. 已知点M（﹣2，3）在双曲线y= $\text{[math]}$ 上，k的值为

查看解析收藏纠错

+选题
14. 一个扇形的圆心角为60°，它所对的弧长为2πcm，则这个扇形的半径为 cm．

查看解析收藏纠错

+选题
15. 将抛物线y=2x²向右平移3个单位，再向下平移4个单位后所得到的抛物线解析式为

查看解析收藏纠错

+选题
16. 在一个不透明的口袋中装有除颜色外其它都相同的5个红球和3个自球，任意从口袋中摸出一个球来，摸到白球的概率为

查看解析收藏纠错

+选题
17.
如图，AB为⊙0的直径，点C、D在⊙0上，且∠ADC=52°，则∠BAC=°．

查看解析收藏纠错

+选题
18.
如图，在Rt△ABC中，∠ACB=90°，∠A=40°，以直角顶点C为旋转中心，将△ABC逆时针旋转到△A′B′C的位置，其中A′、B′分别是A、B的对应点，且点B在斜边A′B′上，直角边CA′交AB于D，则旋转角∠A CA′的度数为．

查看解析收藏纠错

+选题
19. 圆的内接等腰三角形ABC，圆的半径为10，如果底边BC的长为16，那么△ABC的面积为

查看解析收藏纠错

+选题
20.
在四边形ABCD中，AB=CD，M、N分别是AD和BC的中点，延长BA和CD分别交射线NM于点E和点F，若tan∠F= $\text{[math]}$ ， FC=FN，EN= $\text{[math]}$ ，则EF=

查看解析收藏纠错

+选题

21. 先化简，再求代数式 $\text{[math]}$ 的值，其中a=3tan30°+1，b= $\text{[math]}$ cos45°．

查看解析收藏纠错

+选题

22.
如图，网格中每个小正方形的顶点叫格点，△OAB的顶点的坐标分别为O（0，0）、A（1，3）、B（5，0）．
（1）请画出与△OAB关于原点对称的△OCD；（其中A的对称点为C，B的对称点为D）
（2）在（1）的条件下，连接BC、DA，请画出一条直线MN（不与直线AC和坐标轴重合），将四边形ABCD的面积分成相等的两部分，其中M、N分别在AD和BC上，且M、N均为格点，并直接写出直线MN的解析式（写出一个即可）．

查看解析收藏纠错

+选题
23.
如图，小平为了测量学校教学楼的高度，她先在A处利用测角仪测得楼顶C的仰角为30°，再向楼的方向直行50米到达B处，又测得楼顶C的仰角为60度．已知测角仪的高度是1.2米，请你帮助小平计算出学校教学楼的高度CO．（ $\text{[math]}$ ）

查看解析收藏纠错

+选题
24.
已知，在菱形ABCD中，∠ADC=60°，点H为CD上任意一点（不与C、D重合），过点H作CD的垂线，交BD于点E，连接AE．
（1）如图1，线段EH、CH、AE之间的数量关系是；
（2）如图2，将△DHE绕点D顺时针旋转，当点E、H、C在一条直线上时，求证：AE+EH=CH

查看解析收藏纠错

+选题
25. 小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里，据预测，海鲜的市场价格将每天每千克上涨1元．冷冻存放这批海鲜每天需要支出各种费用合计310元，而且这些海鲜在冷库中最多存放160天，同时平均每天有3千克的海鲜变质．
（1）设x天后每千克该海鲜的市场价格为y元，试写出y与x之间的函数关系式；
（2）若存放x天后，将这批海鲜一次性出售．设这批海鲜的销售总额为P元，试写出P与x之间的函数关系式；
（3）小李将这批海鲜存放多少天后出售可获得最大利润，最大利润是多少元？（利润W=销售总额﹣收购成本﹣各种费用）

查看解析收藏纠错

+选题
26.
已知：AB是⊙O的直径，DA、DC分别是⊙O的切线，点A、C是切点，连接DO交弧AC于点E，连接AE、CE．

（1）如图1，求证：EA=EC；
（2）如图2，延长DO交⊙O于点F，连接CF、BE交于点G，求证：∠CGE=2∠F；
（3）如图3，在（2）的条件下，DE= $\text{[math]}$ AD，EF=2 $\text{[math]}$ ，求线段CG的长．

查看解析收藏纠错

+选题
27.
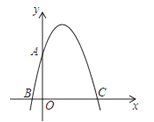
如图，在平面直角坐标系中，点0为坐标原点，抛物线y=ax²+bx+4与y轴交于点A，与x轴交于点B、C（点B在点C左侧），且OA=OC=4OB．
（1）求a，b的值；
（2）连接AB、AC，点P是抛物线上第一象限内一动点，且点P位于对称轴右侧，
过点P作PD⊥AC于点E，分别交x、y轴于点D、H，过点P作PG∥AB交AC于点F，交x轴于点G，设P（x，y），线段DG的长为d，求d与x之间的函数关系（不要求写出自变量x的取值范围）；
（3）在（2）的条件下，当 $\text{[math]}$ 时，连接AP并延长至点M，连接HM交AC于点S，点R是抛物线上一动点，当△ARS为等腰直角三角形时．求点R的坐标和线段AM的长．

查看解析收藏纠错

+选题

2015-2016学年黑龙江省哈尔滨市道里区九年级上学期期末数学试卷

一、单选题

二、填空题

三、计算题

四、解答题

相关试卷收起∨

2015-2016学年黑龙江省哈尔滨市道里区九年级上学期期末数学试卷

一、单选题

二、填空题

三、计算题

四、解答题

相关试卷 收起∨

相关试卷收起∨