广东省佛山市顺德区杏坛中学2019-2020学年七年级下学期数学6月月考试卷

1. 下列计算正确的是（）

A . （a³）²=a⁵ B . （﹣2m³）²=4m⁶ C . a⁶÷a²=a³ D . （a+b）²=a²+b²

查看解析收藏纠错

+选题
2. 将0.00000573用科学记数法表示为（）

A . 0.573×10^﹣⁵ B . 5.73×10^﹣⁵ C . 5.73×10^﹣⁶ D . 0.573×10^﹣⁶

查看解析收藏纠错

+选题
3. 一个角的余角是44°，这个角的补角是（）

A . 134° B . 136° C . 156° D . 146°

查看解析收藏纠错

+选题
4. 下列乘法公式运用正确的是（）

A . （a+b）（b﹣a）＝a²﹣b² B . （﹣m+1）（﹣m﹣1）＝m²﹣1 C . （2x﹣1）²＝2x²+4x﹣1 D . （a+1）²＝a²+1

查看解析收藏纠错

+选题
5. 下列乘法中，不能运用平方差公式进行运算的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 下列事件中，属于必然事件的是（）

A . 打开电视，正在播广告 B . 在一个只装有红球的袋中摸出白球 C . 射击运动员射击一次，命中10环 D . 投掷一枚普通的骰子，掷得的点数小于10

查看解析收藏纠错

+选题
7. 将一个内角为30°的三角板按如图所示放置，已知直线1₁∥l₂ ， ∠1＝80°，则∠2的度数为（）

A . 20° B . 23° C . 25° D . 30°

查看解析收藏纠错

+选题
8. 如图，下列条件：①∠1=∠2；②∠3=∠4；③∠B=∠5；④∠1+∠ACE=180°.其中，能判定AD∥BE的条件有（）

A . 2个 B . 3个 C . 4个 D . 1个

查看解析收藏纠错

+选题
9. 图①是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图②那样拼成一个正方形，则中间空的部分的面积是（）

A . ab B . a²+2ab+b² C . a²﹣b² D . a²﹣2ab+b²

查看解析收藏纠错

+选题
10. 如图，若AB∥CD，CD∥EF，那么∠BCE＝（）

A . ∠1＋∠2 B . ∠2－∠1 C . 180°－∠1＋∠2 D . 180°－∠2＋∠1

查看解析收藏纠错

+选题

11. 在同一平面内，三条直线a、b、c，若a∥b，a∥c，则．

查看解析收藏纠错

+选题
12. （3a²﹣6ab）÷3a=．

查看解析收藏纠错

+选题
13. 若（x-2）（x+3）=x²+px+q,则p+q=.

查看解析收藏纠错

+选题
14. 从一副拿掉大、小王的扑克牌中，抽取一张，抽到红桃的概率是.

查看解析收藏纠错

+选题
15. 有8张卡片，标号为1，2，3，4，5，6，7，8从中任意抽取一张，P（抽到大于3）＝．

查看解析收藏纠错

+选题
16. 已知a+b=7，ab=2，则a²+b²=．

查看解析收藏纠错

+选题
17. 如图所示，AB∥CD，EC⊥CD．若∠BEC＝30°，则∠ABE的度数为．

查看解析收藏纠错

+选题

18. 计算：

（1）计算：（﹣1）²⁰²⁰+|﹣9|﹣（π﹣3.14）⁰ ．

（2） 2019²﹣2018×2020．（用乘法公式简便计算）

查看解析收藏纠错

+选题
19. 先化简，再求值：[（x+y）²+y（2x﹣y）﹣8xy]÷2x，其中x＝2，y＝﹣1．

查看解析收藏纠错

+选题
20. 阅读下面的推理过程，在括号内填上推理的依据，如图：

∵∠1+∠2=180°，∠2+∠4=180°（已知）

∴∠1=∠4（）

∴c∥a（）

又∵∠2+∠3=180°（已知）

∠3=∠6（）

∴∠2+∠6=180°（）

∴a∥b（）

∴c∥b（）

查看解析收藏纠错

+选题
21. 如图，∠AFD=∠1，AC∥DE，

（1）试说明：DF∥BC；

（2）若∠1=68°，DF平分∠ADE，求∠B的度数.

查看解析收藏纠错

+选题
22. 一个口袋中装有3个白球、5个红球,这些球除了颜色外完全相同,充分摇匀后随机摸出一球,发现是白球.

（1）如果将这个白球放回,再摸出一球,它是白球的概率是多少?

（2）如果将这个白球不放回,再摸出一球,它是白球的概率是多少?

查看解析收藏纠错

+选题
23. 我们知道，图形是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数量关系，对几何图形做出代数解释和用几何图形的面积表示代数恒等式是互逆的．课本上由拼图用几何图形的面积来验证了乘法公式，一些代数恒等式也能用这种形式表示，例如（2a＋b）（a＋b）＝2a²＋3ab＋b²就可以用图①或图②等图形的面积表示．

（1）填一填：请写出图③所表示的代数恒等式：；

（2）画一画：试画出一个几何图形，使它的面积能表示：（a＋b）（a＋3b）＝a²＋4ab＋3b².

查看解析收藏纠错

+选题
24. 从边长为 a 的正方形剪掉一个边长为 b 的正方形（如图 1），然后将剩余部分拼成一个长方形（如图 2）．

（1）上述操作能验证的等式是_______（请选择正确的一个）

A . a²﹣2ab+b² ＝（a﹣b）² B . a²﹣b²＝（a+b）（a﹣b） C . a² +ab＝a（a+b）

（2）若 x² ﹣9y²＝12，x+3y＝4，求 x﹣3y 的值；

（3）计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
25. 按要求作答：

（1）问题情境1：如图1，AB∥CD，P是ABCD内部一点，P在BD的右侧，探究∠B，∠P，∠D之间的关系？

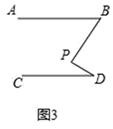
小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠B，∠P，∠D之间满足系．（直接写出结论）

（2）问题情境2：如图3，AB∥CD，P是AB，CD内部一点，P在BD的左侧，可得∠B，∠P，∠D之间满足关系．（直接写出结论）

（3）问题迁移：请合理的利用上面的结论解决以下问题：
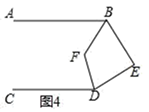
已知AB∥CD，∠ABE与∠CDE两个角的角平分线相交于点F

①如图4，若∠E＝80°，求∠BFD的度数；

②如图5中，∠ABM＝ $\text{[math]}$ ∠ABF，∠CDM＝ $\text{[math]}$ ∠CDF，写出∠M与∠E之间的数量关系并证明你的结论．

③若∠ABM＝ $\text{[math]}$ ∠ABF，∠CDM＝ $\text{[math]}$ ∠CDF，设∠E＝m°，用含有n，m°的代数式直接写出∠M的值．

查看解析收藏纠错

+选题

广东省佛山市顺德区杏坛中学2019-2020学年七年级下学期数学6月月考试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

广东省佛山市顺德区杏坛中学2019-2020学年七年级下学期数学6月月考试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨