江苏省南京市鼓楼区2019-2020学年八年级下学期数学期末考试试卷

1. 化简 $\text{[math]}$ 的结果是（）

A . －2 B . 2 C . －4 D . 4

查看解析收藏纠错

+选题
2. 若分式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . x＞0 B . x≠0 C . x＞1 D . x≠1

查看解析收藏纠错

+选题
3. 在下列事件中，是必然事件的是（）

A . 3天内将下雨 B . 367人中至少有2人的生日相同 C . 买一张电影票，座位号是奇数号 D . 在某妇幼保健医院里，下一个出生的婴儿是女孩

查看解析收藏纠错

+选题
4. 南京奥林匹克体育中心是亚洲A级体育馆、世界第五代体育建筑的代表.如图是体育馆俯视图的示意图.下列说法正确的是（）

A . 这个图形是轴对称图形，但不是中心对称图形 B . 这个图形是中心对称图形，但不是轴对称图形 C . 这个图形既是中心对称图形，也是轴对称图形 D . 这个图形既不是中心对称图形，也不是轴对称图形

查看解析收藏纠错

+选题
5. 已知点P(x₁ ， y₁)、Q(x₂ ， y₂)在反比例函数y＝－ $\text{[math]}$ 的图象上，若y₁＜y₂＜0，则x₁与x₂的大小关系是（）

A . x₁＜x₂ B . x₁＞x₂ C . x₁＝x₂ D . 无法确定

查看解析收藏纠错

+选题
6. 如图，在四边形ABCD中，AD//BC，AD＝6cm，BC＝12cm，点P从A出发以1cm/s的速度向D运动，点Q从C出发以2cm/s的速度向B运动.两点同时出发，当点P运动到点D时，点Q也随之停止运动.若设运动的时间为t秒，以点A，B，C，D，P，Q任意四个点为顶点的四边形中同时存在两个平行四边形，则t的值是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

7. 化简： $\text{[math]}$ ＝.

查看解析收藏纠错

+选题
8. 若式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

查看解析收藏纠错

+选题
9. 方程(x－1)^－¹＝2的解是.

查看解析收藏纠错

+选题
10. 某种油菜籽在相同条件下发芽试验的结果如下：

每批粒数

50

100

300

400

600

1000

发芽的频数

45

96

283

380

571

948

这种油菜籽发芽的概率的估计值是.（结果精确到0.01）

查看解析收藏纠错

+选题
11. 比较大小：4－ $\text{[math]}$ $\text{[math]}$ .（填“＞”、“＜”或“＝”）

查看解析收藏纠错

+选题
12. 如图，在△ABC中，∠ACB＝90°，AB＝13cm，BC＝12cm，点D在边AB上，AD＝AC，AE⊥CD，垂足为E，点F是BC的中点，则EF＝cm.

查看解析收藏纠错

+选题
13. 如图，在△ABC中，∠C＝90°，△ABC绕点A按顺时针方向旋转26°得到△AED，若AD $\text{[math]}$ BC，则∠BAE＝°.

查看解析收藏纠错

+选题
14. 如图、正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于（1，2），则在第一象限内不等式 $\text{[math]}$ 的解集为.

查看解析收藏纠错

+选题
15. 如图，在矩形纸片ABCD中，AD＝ $\text{[math]}$ ，将矩形纸片折叠，边AD、边BC与对角线BD重合，点A与点C恰好落在同一点处，则矩形纸片ABCD的周长是.

查看解析收藏纠错

+选题
16. 如图，在△ABC中，∠ACB＝90°，AC＝3，BC＝4，将△ABC绕点C顺时针旋转90°得到△A'B'C，若P为边AB上一动点，旋转后点P的对应点为点P'，则线段PP'长度的取值范围是.

查看解析收藏纠错

+选题

17. 计算：

（1） $\text{[math]}$ ；

（2） $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 先化简，再求值： $\text{[math]}$ ，其中a＝－ $\text{[math]}$ .

查看解析收藏纠错

+选题
19. 解方程：

（1） $\text{[math]}$ ；

（2） $\text{[math]}$ .

查看解析收藏纠错

+选题
20. 疫情期间，甲、乙两工厂每小时共做3500个KN95口罩，甲工厂做1600个KN95口罩所用的时间与乙工厂做1200个KN95口罩所用的时间相等.甲、乙两工厂每小时各做多少个KN95口罩？

查看解析收藏纠错

+选题

21. 为了调查某校八年级360名学生的身高情况，随机抽取了20名男生与20名女生的身高数据，得到下列图表（图表中身高分组153cm~158cm表示大于或等于153cm而小于158cm，其他类同）：

八年级20名男生身高频数分布表

身高分组（cm）	频数
153~158	1
158~163	2
163~168	6
168~173	7
173~178	3
178~183	1

（1）写出本次调查的总体与样本；

（2）根据调查结果，绘制抽取的40名学生的身高频数分布直方图；

（3）估计该校八年级学生身高在163cm~183cm范围内的学生人数.

查看解析收藏纠错

+选题

22. 已知∠MAN，按要求完成下列尺规作图（不写作法，保留作图痕迹）：

（1）如图①，B、C分别在射线AM、AN上，求作▱ABDC；

（2）如图②，点O是∠MAN内一点，求作线段PQ，使P、Q分别在射线AM、AN上，且点O是PQ的中点.

查看解析收藏纠错

+选题
23. 在5×5的方格纸中，每个小正方形的边长为1，我们把三个顶点都是格点的三角形称为格点三角形.按要求完成下列问题：

（1）在图①中，以AB为边画一个格点三角形，使其为等腰三角形；

（2）在图②中，以AB为边画一个格点三角形，使其为钝角三角形且周长为6＋3 $\text{[math]}$ ；

（3）如图③，若以AB为边的格点三角形的面积为3，则这个三角形的周长为.

查看解析收藏纠错

+选题
24. 如图，在菱形ABCD中，点O是对角线AC的中点，过点O的直线EF与边AD、BC交于点E、F，∠CAE＝∠FEA，连接AF、CE.

（1）求证：四边形AFCE是矩形；

（2）若AB＝5，AC＝2 $\text{[math]}$ ，直接写出四边形AFCE的面积.

查看解析收藏纠错

+选题
25. 如图，点A、B是反比例函数y＝ $\text{[math]}$ 的图象上的两个动点，过A、B分别作AC⊥x轴、BD⊥x轴，分别交反比例函数y＝－ $\text{[math]}$ 的图象于点C、D，四边形ACBD是平行四边形.

（1）若点A的横坐标为－4.
①直接写出线段AC的长度；

②求出点B的坐标；

（2）当点A、B不断运动时，下列关于□ACBD的结论：①□ACBD可能是矩形；②□ACBD可能是菱形；③□ACBD可能是正方形；④□ACBD的周长始终不变；⑤□ACBD的面积始终不变.其中所有正确结论的序号是.

查看解析收藏纠错

+选题
26. 已知，四边形ABCD是正方形，点E是正方形ABCD所在平面内一动点（不与点D重合），AB＝AE，过点B作DE的垂线交DE所在直线于F，连接CF.

提出问题：当点E运动时，线段CF与线段DE之间的数量关系是否发生改变？

（1）探究问题：
首先考察点E的一个特殊位置：当点E与点B重合（如图①）时，点F与点B也重合.用等式表示线段CF与线段DE之间的数量关系：；

（2）然后考察点E的一般位置，分两种情况：
情况1：当点E是正方形ABCD内部一点（如图②）时；

情况2：当点E是正方形ABCD外部一点（如图③）时.

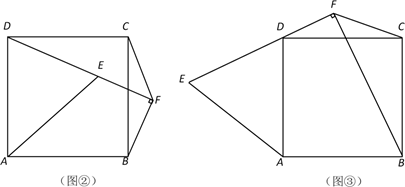
在情况1或情况2下，线段CF与线段DE之间的数量关系与（1）中的结论是否相同？如果都相同，请选择一种情况证明；如果只在一种情况下相同或在两种情况下都不相同，请说明理由；

（3）拓展问题：
连接AF，用等式表示线段AF、CF、DF三者之间的数量关系：.

查看解析收藏纠错

+选题

江苏省南京市鼓楼区2019-2020学年八年级下学期数学期末考试试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

每批粒数	50	100	300	400	600	1000
发芽的频数	45	96	283	380	571	948

江苏省南京市鼓楼区2019-2020学年八年级下学期数学期末考试试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨