2020年浙江省中考数学分类汇编专题12 锐角三角函数

1. 如图，菱形OABC的顶点A，B，C在⊙O上，过点B作⊙O的切线交OA的延长线于点D。若⊙O的半径为1，则BD的长为（）

A . 1 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，在离铁塔150米的A处，用测倾仪测得塔顶的仰角为α，测倾仪高AD为1.5米，则铁塔的高BC为（）

A . (1.5+150tanα) 米 B . (1.5+ $\text{[math]}$ )米 C . (1.5+150sinα)米 D . (1.5+ $\text{[math]}$ )米

查看解析收藏纠错

+选题
3. 已知二次函数y=x²，当a≤x≤b时m≤y≤n，则下列说法正确的是（）

A . 当n-m=1时，b-a有最小值 B . 当n-m=1时，b-a有最大值 C . 当b-a=1时，n-m无最小值 D . 当b-a=1时，n-m有最大值

查看解析收藏纠错

+选题
4. 如图，在△ABC中，∠C=90°，设∠A，∠B，∠C所对的边分别为a，b，c，则（）。

A . c=bsinB B . b=csinB C . a=btanB D . b=ctanB

查看解析收藏纠错

+选题

5. 如图，已知边长为2的等边三角形ABC中，分别以点A，C为圆心，m为半径作弧，两弧交于点D，连结BD。若BD的长为2 $\text{[math]}$ ，则m的值为。

查看解析收藏纠错

+选题
6. 如图是小明画的卡通图形，每个正六边形的边长都相等，相邻两正六边形的边重合，点A，B，C均为正六边形的顶点，AB与地面BC所成的锐角为β，则tanβ的值是.

查看解析收藏纠错

+选题

7. 人字折叠梯完全打开后如图1所示，B，C是折叠梯的两个着地点，D是折叠梯最高级踏板的固定点. 图2是它的示意图，AB=AC，BD=140cm，∠BAC=40°，求点D离地面的高度DE.
（结果精确到0. 1cm；参考数据sin70°≈0. 94，cos70°≈0. 34，sin20°≈0. 34，cos20°≈0. 94）

查看解析收藏纠错

+选题
8. 如图，C，D为⊙O上两点，且在直径AB两侧，连结CD交AB于点E，G是 $\text{[math]}$ 上一点，∠ADC=∠G。

（1）求证：∠1=∠2。

（2）点C关于DG的对称点为F，连结CF.当点F落在直径AB上时，CF=10，tan∠1= $\text{[math]}$ ，求⊙O的半径。

查看解析收藏纠错

+选题
9. 如图1为搭建在地面上的遮阳棚，图2、图3是遮阳棚支架的示意图。遮阳棚支架由相同的菱形和相同的等腰三角形构成，滑块E，H可分别沿等长的立柱AB，DC上下移动，AF=EF=FG=1m。

(结果精确到0.1m，参考数据： $\text{[math]}$ ≈1.73，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)

（1）若移动滑块使AE=EF，求∠AFE的度数和棚宽BC的长。

（2）当∠AFE由60°变为74°时，问棚宽BC是增加还是减少？增加或减少了多少？

查看解析收藏纠错

+选题
10. 有一种升降熨烫台如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图，AB和CD是两根相同长度的活动支撑杆，点O是它们的连接点，OA＝OC，h(cm)表示熨烫台的高度.

（1）如图2—1，若AB＝CD＝110cm，∠AOC＝120°，求h的值；

（2）爱动脑筋的小明发现，当家里这种升降熨烫台的高度为120cm时，两根支撑杆的夹角∠AOC是74°（如图2—2），求该熨烫台支撑杆AB的长度（结果精确到1cm）.（参考数据：sin37°≈0.6，cos37°≈0.8，sin53°≈0.8，cos53°≈0. 6）

查看解析收藏纠错

+选题

11. 为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向。测量方案与数据如下表：

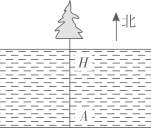
课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
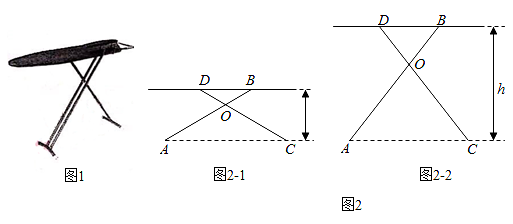
测量方案示意图
说明	点B，C在点A的正东方向	点B，D在点A的正东方向	点B在点A的正东方向，点C在点A的正西方向
测量数据	BC=60m， ∠ABH=70°， ∠ACH=35°	BD=20m， ∠ABH=70°， ∠BCD=35°	BC=101m， ∠ABH=70°， ∠ACH=35°

(参考数据：sin70°≈0.94，sin35°≈0.57，tan70°≈2.75，tan35°≈0.70)

（1）哪个小组的数据无法计算出河宽？

（2）请选择其中一个方案及其数据求出河宽(精确到0.1m)。

查看解析收藏纠错

+选题

12. 图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时，钢条可放入底盒中(底盒固定在地面下)，此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图，经测量，钢条AB=AC=50cm， $\text{[math]}$ .

（1）求车位锁的底盒长BC.

（2）若一辆汽车的底盘高度为30cm，当车位锁上锁时，问这辆汽车能否进入该车位?
(参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ )

查看解析收藏纠错

+选题

2020年浙江省中考数学分类汇编专题12 锐角三角函数

一、单选题

二、填空题

三、综合题

相关试卷收起∨

2020年浙江省中考数学分类汇编专题12 锐角三角函数

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨