河北省保定市竞秀区2016-2017学年中考模拟数学考试试卷

修改时间：2024-07-12 浏览次数：913 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 下列四个数中，最大的一个数是（）

A . 2 B . $\text{[math]}$ C . 0 D . ﹣2

查看解析收藏纠错

+选题
2. 将不等式4x﹣3＜1的解集表示在数轴上，正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列运算正确的是（）

A . a²+a²=a⁴ B . （﹣b²）³=﹣b⁶ C . 2x•2x²=2x³ D . （m﹣n）²=m²﹣n²

查看解析收藏纠错

+选题
4.
如图，若要添加一条线段，使之既是轴对称图形又是中心对称图形，正确的添加位置是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 把0.17×10⁵改写成科学记数法的形式，正确的是（）

A . 17×10³ B . 17×10⁴ C . 1.7×10⁴ D . 1.7×10⁶

查看解析收藏纠错

+选题
6. 如图，是由7个大小相同的小正方体堆砌而成的几何体，若从标有①、②、③、④的四个小正方体中取走一个后，余下几何体与原几何体的主视图相同，则取走的正方体是（）

A . ① B . ② C . ③ D . ④

查看解析收藏纠错

+选题
7. 如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O位似中心，相似比为 $\text{[math]}$ ，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（）

A . （2，1） B . （2，0） C . （3，3） D . （3，1）

查看解析收藏纠错

+选题
8. 若x²﹣3y﹣5=0，则6y﹣2x²﹣6的值为（）

A . 4 B . ﹣4 C . 16 D . ﹣16

查看解析收藏纠错

+选题
9. 如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠ADE=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（）

A . 由小变大 B . 由大变小 C . 不变 D . 先由小变大，后由大变小

查看解析收藏纠错

+选题
10. 已知点A（﹣1，m），B（1，m），C（2，m+1）在同一个函数图象上，这个函数图象可以是（）

A . B . C . D .

查看解析收藏纠错

+选题
11. 用直尺和圆规作Rt△ABC斜边AB上的高线CD，甲、乙两人的作法如图：根据两人的作法可判断（）

A . 甲正确，乙错误 B . 乙正确，甲错误 C . 甲、乙均正确 D . 甲、乙均错误

查看解析收藏纠错

+选题
12. 如图，▱ABCD中，AB=13，AD=10，将▱ABCD沿AE翻折后，点B恰好与点C重合，则点C到AD的距离为（）

A . 5 B . 12 C . 3 D . $\text{[math]}$

查看解析收藏纠错

+选题
13. 如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（）

A . 乙前4秒行驶的路程为48米 B . 在0到8秒内甲的速度每秒增加4米/秒 C . 两车到第3秒时行驶的路程相等 D . 在4至8秒内甲的速度都大于乙的速度

查看解析收藏纠错

+选题
14. 已知函数y=ax²﹣2ax﹣1（a是常数，a≠0），下列结论正确的是（）

A . 当a=1时，函数图象过点（﹣1，1） B . 当a=﹣2时，函数图象与x轴没有交点 C . 若a＞0，则当x≥1时，y随x的增大而减小 D . 不论a为何值，函数图象必经过（2，﹣1）

查看解析收藏纠错

+选题
15. 如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S₁ ，另两张直角三角形纸片的面积都为S₂ ，中间一张正方形纸片的面积为S₃ ，则这个平行四边形的面积一定可以表示为（）

A . 4S₁ B . 4S₂ C . 4S₂+S₃ D . 3S₁+4S₃

查看解析收藏纠错

+选题

二、填空题

16. 计算：（﹣1）⁰+|1﹣ $\text{[math]}$ |=．

查看解析收藏纠错

+选题
17.
如图，以AB为边作正方形ABCD，动点P、Q分别在AB和BC边上运动，且PQ=AB=8，若点Q从点B出发，沿BC向点C运动，则点P随之沿AB下滑，当B到达C点时停止运动．则点Q从B到C的运动过程中，PQ的中点O所经过的路径长为．

查看解析收藏纠错

+选题
18.
如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第2次将点A₁向右平移6个单位长度到达点A₂ ，第3次将点A₂向左移动9个单位长度到达点A₃…则第6次移动到点A₆时，点A₆在数轴上对应的实数是；按照这种规律移动下去，至少移动次后该点到原点的距离不小于41．

查看解析收藏纠错

+选题

三、解答题

19. 下面是小明同学化简代数式a+2+ $\text{[math]}$ 的过程，请仔细阅读并解答所提出的问题．
a+2+ $\text{[math]}$ =2+a+ $\text{[math]}$ …第一步
=（2+a）（2﹣a）+a²…第二步
=2﹣a²+a²…第三步
=2…第四步

（1）小明的解法从第步开始出现错误，正确的化简结果是；

（2）原代数式的值能等于2吗？为什么？

查看解析收藏纠错

+选题
20. 如图：将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F，

（1）求证：△ABF≌△ECF；

（2）若AE=AD，连接AC、BE，求证：四边形ABEC是矩形．

查看解析收藏纠错

+选题
21.
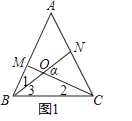
【发现】：如图1，在正三角形ABC中，在AB，AC边上分别取点M，N，BM=AN，连接BN，CM，相交于点O，求∠α
易得：△ABN≌△BCN，则∠1=∠2
∵∠α是△BOC的外角，∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°
【推广】：在正n边形中，对相邻的两边实施同样的操作…

（1）
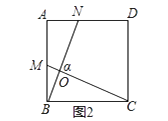
如图2，在正四边形ABCD中，在AB，AD边上分别取点M，N，连接BN，CM，可确定∠α=°；

（2）
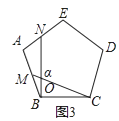
如图3，在正五边形ABCDE中，在AB，AD边上分别取点M，N，连接BN，CM，可确定∠α=°；

（3）判断：∠α可以等于160°吗？如果可以，求出对应的边数n，若不可以，说明理由．

查看解析收藏纠错

+选题
22. 在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示正整数后，背面朝上，洗匀放好，现从中随机抽取一张（不放回），再从剩下的卡片中随机抽取一张．

（1）请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果（卡片用A，B，C，D表示）；

（2）我们知道，满足a²+b²=c²的三个正整数a，b，c成为勾股数，求抽到的两张卡片上的数都是勾股数的概率．

查看解析收藏纠错

+选题
23. 在平面直角坐标系中，反比例函数y= $\text{[math]}$ （x＞0）的图象上有一点A（a，3），过点A作AB⊥x轴于点B，将点B沿x轴正方向平移2个单位长度得到点C，过点C作y轴的平行线交反比例函数于点D，CD= $\text{[math]}$ ，直线AD与x轴交于点M，与y轴交于点N．

（1）用含a的式子表示点D的横坐标为：；

（2）求a的值和直线AD的函数表达式；

（3）请判断线段AN与MD的数量关系，并说明理由；

（4）若一次函数y₁=k₁x+b₁经过点（10，9），与双曲线y= $\text{[math]}$ （x＞0）交于点P，且该一次函数y₁的值随x的增大而增大，请确定P点横坐标n的取值范围（不必写出过程）

查看解析收藏纠错

+选题
24. 某网店3月份经营一种热销商品，每件成本20元，发现三周内售价在持续提升，销售单价P（元/件）与时间t（天）之间的函数关系为P=30+ $\text{[math]}$ t（其中1≤t≤21，t为整数），且其日销售量y（件）与时间t（天）的关系如下表
时间t（天）
1
5
9
13
17
21
日销售量y（件）
118
110
102
94
86
78

（1）已知y与t之间的变化规律符合一次函数关系，请直接写出y（件）与时间t（天）函数关系式；

（2）在这三周的销售中，第几天的销售利润最大？最大日销售利润为多少？

（3）在实际销售的21天中，该网店每销售一件商品就捐赠a元利润（a＜8）给“精准扶贫”的对象，通过销售记录发现，这21天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．

查看解析收藏纠错

+选题
25. 如图，在△ABC中，AB=BC，∠CAB=30°，AC=8，半径为2的⊙O从点A开始（如图1）沿直线AB向右滚动，滚动时始终与直线AB相切（切点为D），当⊙O与△ABC只有一个公共点时滚动停止，作OG⊥AC于点G．

（1）图1中，⊙O在AC边上截得的弦长AE=；

（2）当圆心落在AC上时，如图2，判断BC与⊙O的位置关系，并说明理由．

（3）在⊙O滚动过程中，线段OG的长度随之变化，设AD=x，OG=y，求出y与x的函数关系式，并直接写出x的取值范围．

查看解析收藏纠错

+选题

时间t（天）	1	5	9	13	17	21
日销售量y（件）	118	110	102	94	86	78

河北省保定市竞秀区2016-2017学年中考模拟数学考试试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨