人教版初中数学七年级下学期第一次月考试卷

1. (－2)²的算术平方根是（）

A . 2 B . ±2 C . －2 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 平面上三条直线两两相交最多能构成对顶角的对数是（）.

A . 7 B . 6 C . 5 D . 4

查看解析收藏纠错

+选题
3. －27的立方根与 $\text{[math]}$ 的平方根之和是（）

A . 0 B . －6 C . 0或－6 D . 6

查看解析收藏纠错

+选题
4. 下列语句：①—个数的绝对值—定是正数；② -a—定是—个负数；③绝对值为3的数有两个；④不带根号的数一定是有理数。正确的有 ( )

A . 0个 B . 1个 C . 2个 D . 3个

查看解析收藏纠错

+选题
5.
如图，已知AB∥CD，与∠1是同位角的角是（　　）

A . ∠2 B . ∠3 C . ∠4 D . ∠5

查看解析收藏纠错

+选题
6. 若a²=36，b³=8，则a+b的值是（　　）

A . 8或﹣4 B . +8或﹣8 C . ﹣8或﹣4 D . +4或﹣4

查看解析收藏纠错

+选题
7. 与无理数 $\text{[math]}$ 最接近的整数是（　　）

A . 4 B . 5 C . 6 D . 7

查看解析收藏纠错

+选题
8. 在同一平面内，直线a、b相交于O，b∥c，则a与c的位置关系是（　　）

A . 平行 B . 相交 C . 重合 D . 平行或重合

查看解析收藏纠错

+选题
9. 如图，下列说法中错误的是（　　）

A . ∠3和∠5是同位角 B . ∠4和∠5是同旁内角 C . ∠2和∠4是对顶角 D . ∠1和∠4是内错角

查看解析收藏纠错

+选题
10. 过一点画已知直线的平行线，则( )

A . 有且只有一条 B . 有两条 C . 不存在 D . 不存在或只有一条

查看解析收藏纠错

+选题
11. 已知一个表面积为12dm²的正方体，则这个正方体的棱长为（　　）

A . 1dm B . $\text{[math]}$ dm C . $\text{[math]}$ dm D . 3dm

查看解析收藏纠错

+选题
12. 如图，若直线MN与△ABC的边AB、AC分别交于E、F，则图中的内错角有（　　）

A . 2对 B . 4对 C . 6对 D . 8对

查看解析收藏纠错

+选题

13. 如果一个数的平方根等于这个数的立方根，那么这个数是．

查看解析收藏纠错

+选题
14. 4的算术平方根是，9的平方根是，﹣27的立方根是．

查看解析收藏纠错

+选题
15. 如果一个正数的两个平方根是a+6和2a-15，则这个数为 .

查看解析收藏纠错

+选题
16. 如图所示，与∠C构成同旁内角的有个．

查看解析收藏纠错

+选题

17. 已知某数的平方根是a+3和2a﹣15，求1﹣7a的立方根．

查看解析收藏纠错

+选题
18. 如图，BCD是一条直线，∠1=∠B，∠2=∠A，指出∠1的同位角，∠2的内错角，并求出∠A+∠B+∠ACB的度数．

查看解析收藏纠错

+选题

19. 如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD，

（1）图中除直角外，还有相等的角吗？请写出两对：①；②．

（2）如果∠AOD＝40°，则①∠BOC＝；②OP是∠BOC的平分线，所以∠COP＝度；③求∠BOF的度数．

查看解析收藏纠错

+选题
20. 阅读以下两小题后作出相应的解答：

（1） “同位角相等，两直线平行”，“两直线平行，同位角相等”，这两个命题的题设和结论在命题中的位置恰好对凋，我们把其中一命题叫做另一个命题的逆命题，请你写出命题“角平分线上的点到角两边的距离相等“的逆命题，并指出逆命题的题设和结论；

（2）根据以下语句作出图形，并写出该命题的文字叙述.
已知：过直线AB上一点O任作射线OC ， OM、ON分别平分∠AOC、∠BOC ，则OM⊥ON ．

查看解析收藏纠错

+选题
21. 直线AB、CD相交于点O.OE、OF分别是∠AOC、∠BOD的平分线.

（1）画出这个图形.

（2）射线OE、OF在同一条直线上吗?

（3）画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.

查看解析收藏纠错

+选题
22. 数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人十分惊奇，忙问计算的奥妙．你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：

（1） 10³=1000，100³=1000000，你能确定59319的立方根是几位数吗？答：位数．

（2）由59319的个位数是9，你能确定59319的立方根的个位数是几吗？答：

（3）如果划去59319后面的三位319得到数59，而3³=27，4³=64，由此你能确定59319的立方根的十位数是几吗？答：．因此59319的立方根是．

（4）现在换一个数185193，你能按这种方法说出它的立方根吗？
答：①它的立方根是位数，②它的立方根的个位数是，③它的立方根的十位数是，④185193的立方根是．

查看解析收藏纠错

+选题
23.
如图(2)

（1）如果∠1=∠D，那么∥；

（2）如果∠1=∠B，那么∥；

（3）如果∠A+∠B=18 0º，那么∥；

（4）如果∠A+∠D=180º，那么∥；

查看解析收藏纠错

+选题
24. 如图（1），AB∥CD，猜想∠BPD与∠B，∠D的关系，说出理由．
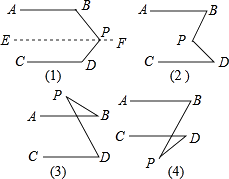
解：猜想∠BPD+∠B+∠D=360°
理由：过点P作EF∥AB，
∴∠B+∠BPE=180°（两直线平行，同旁内角互补）
∵AB∥CD，EF∥AB，
∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）
∴∠EPD+∠D=180°（两直线平行，同旁内角互补）
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°

（1）依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，并说明理由．

（2）观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，不需要说明理由．

查看解析收藏纠错

+选题

人教版初中数学七年级下学期第一次月考试卷

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

人教版初中数学七年级下学期第一次月考试卷

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨