初中数学浙教版九年级下册第一章解直角三角形章末检测

1. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 已知：a为锐角，且 $\text{[math]}$ =1则tana的值等于（）

A . -1 B . 2 C . 3 D . 2.5

查看解析收藏纠错

+选题
3. 若α+β=90°，则正确的是（）

A . sinα﹣sinβ=0 B . sinα﹣cosβ=0 C . cosα﹣cosβ=0 D . cosα+sinβ=0

查看解析收藏纠错

+选题
4. 如果∠A为锐角，cos A= $\text{[math]}$ ，那么（）

A . 0°<∠A<30° B . 30°<∠A<45° C . 45°<∠A<60° D . 60°<∠A<90°

查看解析收藏纠错

+选题
5. 在Rt△ABC中，如果各边长度都扩大3倍，则锐角A的正切值（）

A . 扩大2倍 B . 缩小为原来的 $\text{[math]}$ C . 扩大4倍 D . 没有变化

查看解析收藏纠错

+选题
6. 若 $\text{[math]}$ tan(α+10°)=1，则锐角α的度数是（）

A . 20° B . 30° C . 40° D . 50°

查看解析收藏纠错

+选题
7. 已知tanα=6.866，用计算器求锐角α（精确到1″），按键顺序正确的是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
8. 如图1，在Rt△ABC中，∠ACB=90°，点P以每秒1cm的速度从点A出发，沿折线AC﹣CB运动，到点B停止，过点P作PD⊥AB，垂足为D，PD的长y（cm）与点P的运动时间x（秒）的函数图象如图2所示，当点P运动5秒时，PD的长是（）

A . 2cm B . 1.8cm C . 1.5cm D . 1.2cm

查看解析收藏纠错

+选题
9. 如图，A为某旅游景区的最佳观景点，游客可以在B处乘坐缆车沿BD方向先到达小观景平台DE观景，然后再由E处继续乘坐缆车沿EA方向到达A处，返程时从A处乘坐升降电梯直接到C处．已知AC⊥BC于C，DE∥BC，斜坡BD的坡度i=4：3，BC=210米，DE=48米，BD=100米，α=64°，则AC的高度为（）米（结果精确到0.1米，参考数据：sin64°≈0.9，tan64°≈2.1）

A . 214.2 B . 235.2 C . 294.2 D . 315.2

查看解析收藏纠错

+选题
10. 如图，已知灯塔M方圆一定范围内有镭射辅助信号，一艘轮船在海上从南向北方向以一定的速度匀速航行，轮船在A处测得灯塔M在北偏东30°方向，行驶1小时后到达B处，此时刚好进入灯塔M的镭射信号区，测得灯塔M在北偏东45°方向，则轮船通过灯塔M的镭射信号区的时间为（）

A . （ $\text{[math]}$ ﹣1）小时 B . （ $\text{[math]}$ +1）小时 C . 2小时 D . $\text{[math]}$ 小时

查看解析收藏纠错

+选题

11. 先用计算器求：tan20°≈，tan40°≈，tan60°≈，tan80°≈，再按从小到大的顺序用“＜”把tan20°，tan40°，tan60°，tan80°连接起来：．归纳：正切值，角大值．

查看解析收藏纠错

+选题
12. 在△ABC中，∠C=90°，AC=4，点G为△ABC的重心．如果GC=2，那么sin∠GCB的值是．

查看解析收藏纠错

+选题
13. 因为sin 30°= $\text{[math]}$ 210°=- $\text{[math]}$ ，所以sin 210°=sin(180°+30°)=-sin 30°；因为sin 60°= $\text{[math]}$ ，sin 240°=- $\text{[math]}$ ，所以sin 240°=sin(180°+60°)=-sin 60°；由此猜想、推理知：一般地，当α为锐角时，有sin(180°+α)=-sin α；由此可知sin 225°=.

查看解析收藏纠错

+选题
14. 如图，在平行四边形ABCD中，AE⊥BC，垂足为E，如果AB=5，BC=8， $\text{[math]}$ ，那么EC=.

查看解析收藏纠错

+选题
15. 将一个三角形经过放大后得到另一个三角形，如果所得三角形在原三角形的外部，这两个三角形各对应边平行且距离都相等，那么我们把这样的两个三角形叫做“等距三角形”，它们对应边之间的距离叫做“等距”．如果两个等边三角形是“等距三角形”，它们的“等距”是1，那么它们周长的差是．

查看解析收藏纠错

+选题
16. 如图，从甲楼底部A处测得乙楼顶部C处的仰角是30°，从甲楼顶部B处测得乙楼底部D处的俯角是45°，已知甲楼的高AB是120m，则乙楼的高CD是m（结果保留根号）

查看解析收藏纠错

+选题

17. 计算：

（1） sin²30°＋sin²60°＋1－tan45°

（2） tan²60°－2cos60°－ $\text{[math]}$ sin45°

查看解析收藏纠错

+选题
18. 如图：

（1）已知sinα+cosα= $\text{[math]}$ ，求sinαcosα.

（2）已知α为锐角，tanα=2，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
19. 如图，在△ABC中，∠C=90°，点D、E分别在AC、AB上，BD平分∠ABC，DE⊥AB，AE=6，cos A= $\text{[math]}$ .求：

（1） DE、CD的长；

（2） tan∠DBC的值.

查看解析收藏纠错

+选题
20. 如图①，在Rt△ABC中，以下是小亮探究 $\text{[math]}$ 与 $\text{[math]}$ 之间关系的方法：
∵sinA= $\text{[math]}$ ，sinB= $\text{[math]}$ ，
∴c= $\text{[math]}$ ，c= $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ，
根据你掌握的三角函数知识．在图②的锐角△ABC中，探究 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的关系，并写出探究过程．

查看解析收藏纠错

+选题
21. 如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m）参考数据： $\text{[math]}$ $\text{[math]}$ 1.414， $\text{[math]}$ $\text{[math]}$ 1.732

查看解析收藏纠错

+选题
22. 如图是小红在一次放风筝活动中某时段的示意图，她在A处时的风筝线（整个过程中风筝线近似地看作直线）与水平线构成30°角，线段AA₁表示小红身高1.5米．

（1）当风筝的水平距离AC=18米时，求此时风筝线AD的长度；

（2）当她从点A跑动9 $\text{[math]}$ 米到达点B处时，风筝线与水平线构成45°角，此时风筝到达点E处，风筝的水平移动距离CF=10 $\text{[math]}$ 米，这一过程中风筝线的长度保持不变，求风筝原来的高度C₁D．

查看解析收藏纠错

+选题
23. 如图，海事救援指挥中心A接到海上SOS呼救：一艘渔船B在海上碰到暗礁，船体漏水下沉，5名船员需要援救．经测量渔船B到海岸最近的点C的距离BC=20km，∠BAC=22°37′，指挥中心立即制定三种救援方案（如图1）：
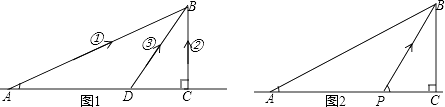
①派一艘冲锋舟直接从A开往B；②先用汽车将冲锋舟沿海岸线送到点C，然后再派冲锋舟前往B；③先用汽车将冲锋舟沿海岸线送到距指挥中心33km的点D，然后再派冲锋舟前往B．
已知冲锋舟在海上航行的速度为60km/h，汽车在海岸线上行驶的速度为90km/h．
（sin22°37′= $\text{[math]}$ ，cos22°37′= $\text{[math]}$ ，tan22°37′= $\text{[math]}$ ）

（1）通过计算比较，这三种方案中，哪种方案较好（汽车装卸冲锋舟的时间忽略不计）？

（2）事后，细心的小明发现，上面的三种方案都不是最佳方案，最佳方案应是：先用汽车将冲锋舟沿海岸线送到点P处，点P满足cos∠BPC= $\text{[math]}$ （冲锋舟与汽车速度的比），然后再派冲锋舟前往B（如图2）．请你说明理由！
如果你反复探索没有解决问题，可以选取①、②、③两种研究方法：
方案①：在线段上AP任取一点M；然后用转化的思想，从几何的角度说明汽车行AM加上冲锋舟行BM的时间比车行AP加上冲锋舟行BP的时间要长．
方案②：在线段上AP任取一点M；设AM=x；然后用含有x的代数式表示出所用时间t；
方案③：利用现有数据，根据cos∠BPC= $\text{[math]}$ 计算出汽车行AP加上冲锋舟行BP的时间．

查看解析收藏纠错

+选题
24. 如图，防洪大堤的横截面ABGH是梯形，背水坡AB的坡度i=1： $\text{[math]}$ （垂直高度AE与水平宽度BE的比），AB=20米，BC=30米，身高为1.7米的小明（AM=1.7米）站在大堤A点（M，A，E三点在同一条直线上），测得电线杆顶端D的仰角∠a=20°．

（1）求背水坡AB的坡角；

（2）求电线杆CD的高度．（结果精确到个位，参考数据sin20°≈0.3，cos20°≈0.9，tan20°≈0.4， $\text{[math]}$ ≈1.7）

查看解析收藏纠错

+选题

初中数学浙教版九年级下册第一章解直角三角形章末检测

一、单选题

二、填空题

三、解答题

相关试卷收起∨

初中数学浙教版九年级下册第一章 解直角三角形 章末检测

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

初中数学浙教版九年级下册第一章解直角三角形章末检测

相关试卷收起∨